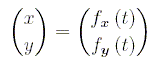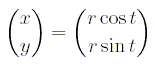![]()
Geometria Reference
Contents
1 Geometrische Objekte / Geometrical Objects
1.1 Ziehbare Punkte / Dragable Points
1.1.1 Punkt in Zeichenfläche / Point in drawing plane
1.1.2 Punkt in Punktmenge
1.1.3 Punkt in Kreis- oder Polygonfläche
1.1.4 Punkt auf Objekt / Point on Object
1.1.5 Horizontal ziehbarer Punkt
1.1.6 Vertikal ziehbarer Punkt
1.1.7 Ecke / Vertex
1.2 Nicht-ziehbare Punkte / Non-dragable Points
1.2.1 Fixpunkt / Fixed Point
1.2.2 Mittelpunkt / Midpoint
1.2.3 Schnittpunkt / Intersection Point
1.2.4 Fußpunkt
1.2.5 Strecke abtragen
1.2.6 Punkt im speziellen Streckenverhältnis
1.2.7 Bildpunkt einer Drehung oder Drehstreckung / Image Point of a rotation
1.2.8 Bildpunkt einer Geraden- oder Schubspiegelung / Image of a line reflection
1.2.9 Bildpunkt einer Streckung oder Punktspiegelung /
Image of a dilation or point reflection
1.2.10 Bildpunkt einer Verschiebung / Image of a translation
1.2.11 Bildpunkt einer Kreisspiegelung
1.2.12 Funktionsabhängiger Punkt / Functiondependent Point
1.2.13 Winkelhalbierendenpunkt
1.2.14 Winkelteilendenpunkt
1.2.15 Vierter Parallelogrammpunkt
1.2.16 Mittelpunkt eines Kreises
1.2.17 Eckpunkt eines Polygons
1.2.18 Endpunkt einer Strecke
1.2.19 Punkt für ähnliche Dreiecke
1.3 Strecke, Strahl, Gerade / Line Segment, Ray, Straight Line
1.3.1 Strecke / Line Segment
1.3.2 Strahl / Ray
1.3.3 Gerade / Straight line
1.3.4 Orthogonale / Perpendicular line
1.3.5 Parallele / Parallel line
1.3.6 Winkelhalbierende / Angle bisector
1.3.7 Winkelteilende / Angle deviding line
1.3.8 Dreieckshöhe
1.3.9 Kreissehne
1.3.10 Kante / Edge
1.4 Kurven / Curves
1.4.1 Parametrisierte Kurven / Parametric curves
1.4.2 Externe Kurven-Klassen / External classes of curves
1.4.3 Ortslinie / Locus
1.4.4 Kegelschnitte
1.5 Kreise / Circles
1.5.1 Kreis / Circle
1.5.2 Inversion eines Kreises an einem Kreis
1.6 Kreissektoren / Sectors of Circles
1.6.1 Kreisbogen / Arc of circle
1.6.2 Winkelbogen / Arc of angle
1.7 Polygone / Polygons
1.7.1 Polygon mit vorgegebenen Eckpunkten / Polygons with predetermined
number of vertices
1.7.2 Gleichseitiges Dreieck
1.7.3 Ähnliches Dreieck
1.7.4 Quadrat
1.7.5 Parallelogramm
1.7.6 Reguläre Polygone
1.7.7 Reguläre Sternpolygone
1.7.8 Graphen / Graphs
1.8 Punktmengen
1.9 Koordinatensysteme / Coordinate Systems
2 Funktionale / Functions
2.1 Hinweise zum Arbeiten mit Funktionalen
2.2 Eigenschaften von Objekten / Object Properties
2.2.1 Eigenschaften von Punkten / Properties of Points
2.2.2 Eigenschaften von Strecken und Geraden / Properties of line segments
and straight lines
2.2.3 Eigenschaften von Kreisen / Properties of circles
2.2.4 Eigenschaften von Polygonen / Properties of Polygons
2.3 Implementierte Funktionale
2.3.1 Abstand
2.3.2 Winkel
2.3.3 Streckenverhältnisse
2.3.4 Ähnlichkeit
2.3.5 Kollinearität
2.3.6 Kongruenz
2.3.7 Inzidenz
2.3.8 Inklusion
2.3.9 Parallelität
2.3.10 Orthogonalität
2.4 Umgang mit Termen / Working with Terms
2.4.1 Termevaluation / Term evaluation
2.4.2 Prüffunktionen / Functions with boolean values
2.4.3 Terme mit Fallunterscheidungen / Terms with case distinctions
2.4.4 Externe Funktionsbibliotheken / External function libraries
2.5 Interaktionselemente / Interaction Elements
2.5.1 Schieberegler / Slide controller
2.5.2 Checkbox / Checkbox
2.5.3 Schalter / Button
3 Sonderfunktionen / Special Functions
3.1 Beschränken des
Zustandsraums der Figur / Restricting the States of Figures
3.2 Ein- und Ausblenden
von Objekten / Showing and Hiding Objects
3.3 Erzeugen von speziellen
Figurenzuständen / Creating Specific States of the Figures
3.4 Hilfen / Help
3.5 Textfenster / Textbox
3.6 Bilder / Pictures
3.7 Antwortanalyse / Response Analysis
3.8 Animationen /
Animations
4 Systemeinstellungen
4.1 Variablen / Variables
4.2 Farbdefinitionen
/ Color Definitions
4.3 Punktformen / Point Shapes
4.4 Sonderzeichen
/ Special Characters
4.5 Applet-Parameter / Applet Parameters
Chapter 1
Geometrische Objekte / Geometrical Objects
1.1 Ziehbare Punkte / Dragable Points
1.1.1 Punkt in Zeichenfläche / Point in drawing plane
Ein Punkt, der frei innerhalb der gesamten Zeichenfläche gezogen werden kann, wird durch die Unterklassen Dragable oder Free realisiert. Als Objektdaten müssen die beiden Anfangskoordinaten angegeben werden.
Points that can be dragged freely within the boundaries of the drawing area are realized by use of the subclasses Dragable or Free. The two starting coordinates are the necessary object data that has to be provided.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
free |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; free; 3.0, 3.0; e[2] = B; point; dragable; 0.0, 0.0;
1.1.2 Punkt in Punktmenge
Ein Punkt, der innerhalb einer Punktmenge gezogen werden kann, wird durch die Unterklasse Dragable realisiert. Als Objektdaten müssen die beiden Anfangskoordinaten und ein Punktmengenobjekt angegeben werden.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Punktmenge [PS] > | |||||||
|
|
|||||||
Beispiel:
e[1] = Pset; line; pointSet; "Kurve01.gif", 10000, 10; e[2] = A; point; dragable; 2.7,5.4, Pset;
1.1.3 Punkt in Kreis- oder Polygonfläche
Ein Punkt, der innerhalb der Fläche eines Kreises oder eines Polygons gezogen werden kann, wird durch die Unterklasse Dragable realisiert. Als Objektdaten müssen die beiden Anfangskoordinaten, ein Kreis- oder Polygonobjekt, das als Bezugsobjekt dient, sowie der Zusatz "area" angegeben werden.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Kreis [C] > , | |||||||
| "area" | |||||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Polygon [PG] > , | |||||||
| "area" | |||||||
|
|
|||||||
Beispiel:
e[1] = P1; point; dragable; 6.0,-1.0; e[2] = P2; point; dragable; 8.0,2.0; e[3] = k1; circle; radius; P1,P2; e[4] = P3; point; dragable; 2.0,-1.0,k1; e[5] = P4; point; dragable; 6.0,-2.0,k1,"area"; e[6] = P5; point; dragable; 0.0,0.0; e[7] = P6; point; dragable; -8.0,2.0; e[8] = P7; point; dragable; -10.0,-7.0; e[9] = P8; point; dragable; 0.0,-7.0; e[10] = p; polygon; polygon; P5,P6,P7,P8; e[11] = P9; point; dragable; -3.0,-2.0,p,"area";
1.1.4 Punkt auf Objekt / Point on object
Mit ''Punkt auf Objekt'' wird ein ziehbarer Punkt bezeichnet, der entlang der Bahn von eindimensionalen Objekten gezogen werden kann. Zu diesen Objekten zählen: Strecken, Strahlen, Geraden, Polygone, Kreise, Kreisbögen, Kurven und Ortslinien. Um einen solchen Punkt erzeugen zu können, müssen als Objektdaten die beiden Anfangskoordinaten und das Bezugsobjekt angegeben werden.
We use the term ''point on object'' to refer to a dragable point that can be dragged along the path of a one-dimensional object. Among these objects we count: line segments, rays, straight lines, polygons, circles, arcs of circles, curves, and loci. In order to create such a point the two starting coordinates and the object of reference have to be provided as object data.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Strecke [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Strahl [R] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Gerade [ST] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Kreis [C] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Kreisbogen [SE] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Polygon [PG] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Kurve [CU] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
dragable |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > , | |||||||
| < Ortslinie [LO] > | |||||||
|
|
|||||||
Beispiel:
e[1] = P1; point; dragable; -9.9,8.9; e[2] = P2; point; dragable; 7.0,9.0; e[3] = s1; line; straightLine; P1,P2; e[4] = P3; point; dragable; -5.0,4.0,s1;
1.1.5 Horizontal ziehbarer Punkt
Ein Punkt, der nur horizontal ziehbar ist, wird durch die Unterklasse Horizontal realisiert. Dazu muß ein Punkt P angegeben werden, von dem der ziehbare Punkt abhängig ist und der den Wert der y-Koordinate bestimmt. Außerdem ist ein Initialisierungswert für die x-Koordinate festzulegen.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
horizontal |
< Punkt [P] > , |
||||
| < x-Koordinate [d] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 0.0,-5.0; e[2] = H; point; horizontal; A,3.0;
1.1.6 Vertikal ziehbarer Punkt
Ein Punkt, der nur vertikal ziehbar ist, wird durch die Unterklasse Vertical realisiert. Dazu muß ein Punkt P angegeben werden, von dem der ziehbare Punkt abhängig ist und der den Wert der x-Koordinate bestimmt. Außerdem ist ein Initialisierungswert für die y-Koordinate festzulegen.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
vertical |
< Punkt [P] > , |
||||
| < y-Koordinate [d] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 0.0,-5.0; e[2] = V; point; vertical; A,3.0;
1.1.7 Ecke / Vertex
Ein ziehbarer Punkt in der Unterklasse Vertex ist insbesonderefür die Visualisierung von mathematischen Graphen entwickelt.
Es ist daher erforderlich, bei der Definition ein Objekt der
Klasse Graph anzugeben. Ferner müssen die Start-Koordinaten
definiert sein.
A dragable point object in the subclass vertex is especially
defined for the visualisation of mathematical graphs. So it is
nessessary to refer to a graph object in the construction data.
Also there must be given the start coordinates.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
vertex |
< Graph-Object > , |
||||
| < x-Coordinate [d] >,< y-Coordinate [d] > | |||||||
|
|
|||||||
Beispiel:
e[1] = graph; polygon; graph; "";
e[2] = X1; point; vertex; graph,-5.0,4.0;
e[3] = X2; point; vertex; graph,4.1,-2.75;
1.2 Nicht-ziehbare Punkte / Non-dragable Points
1.2.1 Fixpunkt / Fixed point
Ein Fixpunkt besitzt eine feste Lage in der Zeichenfläche und kann nicht verschoben werden. Als Objektdaten sind zwei Koordinatenwerte anzugeben.
A fixed point is, as the name suggestst, in a fixed position within the drawing plane and cannot be dragged. Object data that has to be determined are the values of the two coordinates.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
fixed |
< x-Koordinate [d] > , |
||||
| < y-Koordinate [d] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; fixed; 1.0,1.0; e[2] = B; point; fixed; 0.0,0.0;
1.2.2 Mittelpunkt / Midpoint
Den Mittelpunkt zwischen zwei Punkten erhält man durch die Unterklasse Midpoint. Als Objektdaten müssen zwei Punkte übergeben werden.
The subclass Midpoint generates the midpoint between to points. The object data that needs to be provided are the two points.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
midpoint |
< Punkt [P] > , |
||||
| < Punkt [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = M; point; midpoint; A,B;
1.2.3 Schnittpunkt / Intersection point
Schnittpunkte zwischen Strecken, Strahlen, Geraden und Kreisen werden durch die Klasse Intersection erzeugt. Beim Schnitt eines Kreises mit einem zweiten Objekt, werden die Schnittpunkte durch Angabe der Werte 1 oder 2 unterschieden. Hier gibt es außerdem noch einen softwaretechnisch besonderen Fall: Wenn in einer speziellen Figurenkonstruktion bereits ein Schnittpunkt durch einen ziehbaren Punkt, der z. B. den Radius bestimmt, festgelegt ist, dann bewirkt die Angabe des Werts -1, daß der neu zu erzeugende Schnittpunkt nicht mit dem vorhandenen zusammenfällt.
Intersection points between sections of lines, rays, straight lines, and circles are generated by the class Intersection. When a circle intersects with a second object the intersections are distinguished by use of two values, 1 and 2.
In addition, a special case has been implemented into the software: If
in a special construction of two objects an intersection is already determined
by a dragable point, which might determine the radius for example, then
use of the value –1 will provide that the intersection which is to
be generated will be different from the first one.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
intersection |
< Strecke, Strahl |
||||
| oder Gerade [L] > , | |||||||
| < Strecke, Strahl | |||||||
| oder Gerade [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
intersection |
< Strecke, Strahl |
||||
| oder Gerade [L] > , | |||||||
| < Kreis [C] > , | |||||||
| < 1. oder 2. Lsg. [i] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
intersection |
< Kreis [C] > , |
||||
| < Kreis [C] > , | |||||||
| < 1. oder 2. Lsg. [i] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 8.0,8.0; e[4] = D; point; dragable; 5.0,-3.0; e[5] = E; point; dragable; 0.0,3.0; e[6] = g; line; straightLine; A,B; e[7] = k; circle; circumcircle; C,D,E; e[8] = I1; point; intersection; g,k,1; e[9] = I2; point; intersection; g,k,2;
1.2.4 Fußpunkt
Zu einem Punkt A und einer Geraden BC kann mit Hilfe der Unterklasse Foot ein Fußpunkt D erzeugt werden, so daß die Gerade DA orthogonal zu BC ist.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
foot |
< Punkt A [P] > , |
||||
| < Gerade BC [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
foot |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0; e[2] = B; point; dragable; 0.0,4.0; e[3] = C; point; dragable; 2.0,3.0; e[4] = g; line; straightLine; B,C; e[5] = D; point; foot; A,g;
1.2.5 Strecke abtragen
Mit Hilfe der beiden Unterklassen Cutoff und Extend lassen sich Strecken abtragen. Im ersten Fall werden die beiden Strecken AB und CD betrachtet. Dazu wird ein Punkt E erzeugt, indem die Strecke CD von A aus in Richtung auf B abgetragen wird, so daß |AE| = |CD|. Im zweiten Fall werden wiederum zwei Strecken AB und CD betrachtet. Dazu wird ein Punkt E erzeugt, indem die Strecke CD von B aus in die zu A entgegengesetzte Richtung abgetragen wird, so daß |BE| = |CD|.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
cutoff |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < Punkt D [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
cutoff |
< Strecke AB [L] > , |
||||
| < Strecke CD [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
extend |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < Punkt D [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
extend |
< Strecke AB [L] > , |
||||
| < Strecke CD [L] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0; e[2] = B; point; dragable; 0.0,4.0; e[3] = C; point; dragable; 2.0,3.0; e[4] = D; point; dragable; 1.0,1.0; e[5] = E; point; cutoff; A,B,C,D; e[6] = F; point; extend; A,B,C,D;
1.2.6 Punkt im speziellen Streckenverhältnis
Mit Hilfe der beiden Unterklassen Proportion und MeanProportional lassen sich spezielle Streckenverhältnisse abtragen. Im ersten Fall werden die vier Strecken AB, CD, EF und GH betrachtet. Dazu wird ein Punkt I erzeugt, der auf der Strecke GH liegt und für den gilt:
|
|
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
proportion |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < Punkt D [P] > , | |||||||
| < Punkt E [P] > , | |||||||
| < Punkt F [P] > , | |||||||
| < Punkt G [P] > , | |||||||
| < Punkt H [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
proportion |
< Strecke AB [L] > , |
||||
| < Strecke CD [L] > , | |||||||
| < Strecke EF [L] > , | |||||||
| < Strecke GH [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
meanProportional |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < Punkt D [P] > , | |||||||
| < Punkt E [P] > , | |||||||
| < Punkt F [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
meanProportional |
< Strecke AB [L] > , |
||||
| < Strecke CD [L] > , | |||||||
| < Strecke EF [L] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0; e[2] = B; point; dragable; 0.0,4.0; e[3] = C; point; dragable; 2.0,3.0; e[4] = D; point; dragable; 1.0,1.0; e[5] = E; point; dragable; 3.0,2.0; e[6] = F; point; dragable; 0.0,0.0; e[7] = G; point; meanProportional; A,B,C,D,E,F;
1.2.7 Bildpunkt einer Drehung oder Drehstreckung / Imagepoint of a rotation
Der Bildpunkt einer Drehung oder Drehstreckung wird durch die Unterklasse Rotation realisiert. Für die Drehung sind als Objektdaten ein Punkt P als Urbild und ein Punkt Z als Drehzentrum anzugeben. Der Drehwinkel j kann durch einen konstanten Wert, durch ein veränderliches Funktional oder durch drei Punkte mit j = ÐABC definiert sein. Außerdem ist ein Streckfaktor s festzulegen. Soll keine Streckung ausgeführt werden, so ist s = 1.0 zu setzen oder einfacher: man gibt keinen Wert für s an.
The image point of a rotation or dilation is implemented in the subclass Rotation. For a rotation the original point P and a point Z as the center point of rotaion has to be determined. The angle of rotation j can be defined by a constant value, a function, or three points with j = ÐABC. Additionally a dilation factor s can be determined. If no deletion is wanted s can be set to s = 1.0. Or even easier: s can simply be omitted altogether.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
rotation |
< Punkt P [P] > , |
||||
| < Punkt Z [P] > , | |||||||
| < Drehwinkel j [d] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
rotation |
< Punkt P [P] > , |
||||
| < Punkt Z [P] > , | |||||||
| < Drehwinkel j [d] > , | |||||||
| < Streckfaktor s [d] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
rotation |
< Punkt P [P] > , |
||||
| < Punkt Z [P] > , | |||||||
| < Drehwinkel j [M] > , | |||||||
| < Streckfaktor s [M] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
rotation |
< Punkt P [P] > , |
||||
| < Punkt Z [P] > , | |||||||
| < Punkt A [P] > , | |||||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < Streckfaktor s [d] > | |||||||
|
|
|||||||
Beispiel:
e[1] = P; point; dragable; 1.0,1.0; e[2] = Z; point; dragable; 0.0,0.0; e[3] = A; point; dragable; 1.0,3.0; e[4] = B; point; dragable; 0.0,4.0; e[5] = C; point; dragable; 4.0,5.0; e[6] = P'; point; rotation; P,Z,3.14; e[7] = P''; point; rotation; P,Z,A,B,C;
1.2.8 Bildpunkt einer Geraden- oder Schubspiegelung / Image of a line reflection
Der Bildpunkt einer Geraden- oder Schubspiegelung wird durch die Unterklasse Mirror realisiert. Für eine Geradenspiegelung ist ein Urbildpunkt P und eine Gerade g anzugeben, die als Spiegelachse dient. Für eine Schubspiegelung sind neben P und g zwei Werte für die x- und y-Translation festzulegen.
The image of a line reflection or translation is implemented in the subclass Mirror. For a line reflection the original point P and the line g, which functions as the mirror axis, has to be determined. For a translation aside of P und g two additional values, x- und y-translation, have to be determined.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
mirror |
< Punkt P [P] > , |
||||
| < Gerade g [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
mirror |
< Punkt P [P] > , |
||||
| < Gerade g [L] > , | |||||||
| < x-Translation [d] > , | |||||||
| < y-Translation [d] > | |||||||
|
|
|||||||
Beispiel:
e[1] = P; point; dragable; 1.0,1.0; e[2] = A; point; dragable; -9.0,8.0; e[3] = B; point; dragable; 7.0,9.0; e[4] = g; line; straightLine; A,B; e[5] = P'; point; mirror; P,g; e[6] = P''; point; mirror; P,g,1.5,1.5;
1.2.9 Bildpunkt einer Streckung oder Punktspiegelung / Image of a dilation or point reflection
Der Bildpunkt einer Streckung und einer Punktspiegelung wird durch die Unterklasse Mirror realisiert. Für die Streckung sind als Objektdaten ein Punkt P als Urbild, ein Punkt Z als Streckzentrum sowie ein Streckfaktor s anzugeben. Die Punktspiegelung benötigt nur die Angabe von P und Z.
The image point of a dilation and a reflection is implemented in the subclass Mirror. For the dilation an original point P, a point Z, as the center of dilation, and a factor of dilation s. For a reflection only the points P and Z are needed.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
mirror |
< Punkt P [P] > , |
||||
| < Punkt Z [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
mirror |
< Punkt P [P] > , |
||||
| < Punkt Z [P] > , | |||||||
| < Streckfaktor s [d] > | |||||||
|
|
|||||||
Beispiel:
e[1] = P; point; dragable; 1.0,1.0; e[2] = Z; point; dragable; 0.0,0.0; e[3] = P'; point; mirror; P,Z; e[4] = P''; point; mirror; P,Z,1.5;
1.2.10 Bildpunkt einer Verschiebung / Image of a translation
Der Bildpunkt einer Verschiebung wird durch die Unterklasse Translation realisiert. Für die Verschiebung müssen als Objektdaten ein Urbildpunkt P und ein Verschiebevektor v angegeben werden. Der Vektor kann dabei durch zwei konstante Werte vx und vy oder durch zwei Punkte V1 und V2 definiert werden.
The image of a translation and a point reflection is implemented in the subclass Translation. For the dilation an original point P and the vector of the translation v has to be determined. The vector can be defined by two constant values vx and vy or by two points V1 und V2.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
translation |
< Punkt P [P] > , |
||||
| < vx [d] > , | |||||||
| < vy [d] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
translation |
< Punkt P [P] > , |
||||
| < Punkt V1 [P] > , | |||||||
| < Punkt V2 [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = P; point; dragable; 1.0,1.0; e[2] = A; point; dragable; 0.0,0.0; e[3] = B; point; dragable; 4.0,0.0; e[4] = P'; point; translation; P,4.0,3.0; e[5] = P''; point; translation; P,A,B;
1.2.11 Bildpunkt einer Kreisspiegelung
Der Bildpunkt einer Kreisspiegelung wird durch die Unterklasse Invert realisiert. Als Objektdaten müssen ein Punkt als Urbild und ein Kreis übergeben werden.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
invert |
< Punkt [P] > , |
||||
| < Kreis [C] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 2.0,8.0; e[4] = k; circle; circumcircle; A,B,C; e[5] = P; point; dragable; 4.0,0.0; e[6] = P'; point; invert; P,k;
1.2.12 Funktionsabhängiger Punkt / Functiondependent Point
Funktionsabhängige Punkte werden durch die Klasse FunctionDepend erzeugt. Dazu sind als Objektdaten zwei Koordinatenfunktionen anzugeben, die durch zwei Objekte der Klasse MeasureCalculate definiert werden. Wahlweise kann ein solcher Punkt in einem speziellen Koordinatensystem (Seite pageref) angezeigt werden.
Points that are dependent on functions are generated by the subclass FunctionDepend. Two functions for the coordinates have to be determined, which are defined by two objects of the class MeasureCalculate. By choice a point of that type can be depicted in a coordinate system (pageref).
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
functionDepend |
< Fkt. x-Koord. [M] > , |
||||
| < Fkt. y-Koord. [M] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
functionDepend |
< Fkt. x-Koord. [M] > , |
||||
| < Fkt. y-Koord. [M] > , | |||||||
| < Koordinatensystem [CO] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0;
e[2] = B; point; dragable; 0.0,0.0;
e[3] = C; point; functionDepend; "(coordinateX(A)+coordinateX(B))/2",
"(coordinateY(A)+coordinateY(B))/2";
1.2.13 Winkelhalbierendenpunkt
Zu drei Punkten A, B, C kann man durch die Unterklasse AngleBiSector einen Punkt D erzeugen, der auf der Winkelhalbierenden des Winkels ÐABC liegt.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
angleBiSector |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = D; point; angleBiSector; A,B,C;
1.2.14 Winkelteilendenpunkt
Zu drei Punkten A, B, C kann man durch die Unterklasse AngleDivider einen Punkt D erzeugen, der auf der Geraden liegt, die den Winkel ÐABC im Verhältnis 1:n teilt.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
angleDivider |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < n [i] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
angleDivider |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < n [d] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = D; point; angleDivider; A,B,C,3;
1.2.15 Vierter Parallelogrammpunkt
Zu drei Punkten A, B, C kann man mit Hilfe der Unterklasse Parallelogram einen Punkt D erzeugen, so daß ABCD ein Parallelogramm ist.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
parallelogram |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = D; point; parallelogram; A,B,C;
1.2.16 Mittelpunkt eines Kreises
Der Mittelpunkt eines Kreises wird durch die beiden Unterklassen Center und CircumCenter realisiert. Als Objektdaten müssen entweder ein Kreis oder drei Punkte übergeben werden.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
center |
< Kreis [C] > |
||||
|
|
|||||||
|
< Name [s] > |
point |
circumCenter |
< Punkt [P] > , |
||||
| < Punkt [P] > , | |||||||
| < Punkt [P] > , | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 2.0,8.0; e[4] = k; circle; circumcircle; A,B,C; e[5] = M; point; center; k;
1.2.17 Eckpunkt eines Polygons
Zugriff auf den n-ten Eckpunkt eines Polygons erhält man durch die Unterklasse Vertex. Als Objektdaten müssen ein Polygon und der Wert n übergeben werden.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
vertex |
< Polygon [PG] > , |
||||
| < n [i] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = p; polygon; square; A,B; e[4] = C; point; vertex; p,3; e[5] = D; point; vertex; p,4;
1.2.18 Endpunkt einer Strecke
Durch die Unterklassen First und Last erhält man Zugriff auf die beiden Endpunkte einer Strecke.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
first |
< Strecke [L] > |
||||
|
|
|||||||
|
< Name [s] > |
point |
last |
< Strecke [L] > |
||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0; e[2] = B; point; dragable; 0.0,4.0; e[3] = k1; circle; radius; A,B; e[4] = C; point; dragable; 2.0,3.0; e[5] = D; point; dragable; 2.0,4.0; e[6] = k2; circle; radius; C,D; e[7] = s; line; bichord; k1,k2; e[8] = P1; point; first; s; e[9] = P2; point; last; s;
1.2.19 Punkt für ähnliche Dreiecke
Mit Hilfe der Unterklasse Similar läßt sich zu einem Dreieck ABC und zwei Punkten D und E ein dritter Punkt F erzeugen, so daß ABC und DEF zueinander ähnlich sind.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
similar |
< Punkt D [P] > , |
||||
| < Punkt E [P] > , | |||||||
| < Punkt A [P] > , | |||||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0; e[2] = B; point; dragable; 0.0,4.0; e[3] = C; point; dragable; 2.0,3.0; e[4] = D; point; dragable; 1.0,1.0; e[5] = E; point; dragable; 3.0,2.0; e[6] = F; point; similar; D,E,A,B,C;
1.3 Strecke, Strahl, Gerade / Line Segment, Ray, Straight Line
1.3.1 Strecke / Line Segment
Eine Strecke wird definiert durch zwei Punkte A und B. Durch die optionale Angabe zweier Zeichenketten s1 und s2 kann die Länge der Strecke gemessen und auf der Zeichenfläche ausgegeben werden. Dabei werden s1 und s2 vor und hinter dem Wert der Streckenlänge angezeigt.
A line segment is defined by two points A and B. By use of the two strings s1 and s2, which is optional, the length of the segment can be calculated and printed to the displayed in the drawing area. s1 and s2 will then be displayed in front of and behind the value of the segment’s length.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
connect |
< Punkt A [P] > , |
||||
| < Punkt B [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
connect |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Präfix s1 [s] > , | |||||||
| < Postfix s2 [s] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = s; line; connect; A,B,"s = "," L.E.";
1.3.2 Strahl / Ray
Ein Strahl wird definiert durch zwei Punkte S und T. Der Strahl beginnt im Punkt S und verläuft durch T.
A ray is defined by two points S and T. The ray has its origin in S and expands through T.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
ray |
< Punkt S [P] > , |
||||
| < Punkt T [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = s; line; ray; A,B;
1.3.3 Gerade / Straight line
Eine Gerade wird definiert durch zwei Punkte A und B.
A straight line is defined by two points A and B.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
straightLine |
< Punkt A [P] > , |
||||
| < Punkt B [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = g; line; straightLine; A,B;
1.3.4 Orthogonale / Perpendicular
line
Eine Orthogonale wird durch die Unterklasse Perpendicular realisiert. Als Objektdaten müssen dazu eine Gerade g und ein Punkt P übergeben werden, so daß eine Orthogonale h erzeugt wird, mit h ^g und P Î h.
A perpendicular line is implemented by the class Perpendicular. A line g and a point P have to be provided so that a perpendicualr line h can be generated, with h ^ g and P Îh.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
perpendicular |
< Punkt P [P] > , |
||||
| < Gerade g [L] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = g; line; straightLine; A,B; e[5] = h; line; perpendicular; C,g;
1.3.5 Parallele / Parallel line
Eine Parallele wird durch die Unterklasse Parallel realisiert. Als Objektdaten müssen dazu eine Gerade g und ein Punkt P übergeben werden, so daß eine Parallele h erzeugt wird, mit h ||g und P Î h.
A parallel line is implemented by the subclass Parallel. A line g and a point P have to be provided so that a parallel line h can be generated, with h || g and P Îh.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
parallel |
< Punkt P [P] > , |
||||
| < Gerade g [L] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = g; line; straightLine; A,B; e[5] = h; line; parallel; C,g;
1.3.6 Winkelhalbierende / Angle bisector
Eine Winkelhalbierende wird durch die Unterklasse AngleBiSector realisiert. Dazu muß ein Winkel ÐABC durch drei Punkte angegeben werden.
Angle bisectors are implemented by the subclass AngleBiSector. The angle ÐABC has to be determined by three points.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
angleBiSector |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = w; line; angleBiSector; A,B,C;
1.3.7 Winkelteilende / Angle deviding line
Eine Winkelteilende ist eine Gerade, die einen Winkel ÐABC im Verhältnis 1:n teilt. Sie wird durch die Unterklasse AngleDivider realisiert. Als Objektdaten sind für den Winkel drei Punkte anzugeben sowie ein Wert für n.
An angle deviding line is a straight line which devides an angle ÐABC in a ratio 1:n. It is implemented by the subclass AngleDivider. The object data that has to be determinded are the three points for the angle and n.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
angleDivider |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < n [d] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = w; line; angleDivider; A,B,C,3.0;
1.3.8 Dreieckshöhe
Die Höhe ha in einem Dreieck ABC wird durch die Unterklasse Foot realisiert. Als Objektdaten sind drei Punkte A, B und C anzugeben.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
foot |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
foot |
< Punkt A [P] > , |
||||
| < Strecke BC [L] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = ha; line; foot; A,B,C; e[5] = c; line; connect; A,B; e[6] = hc; line; foot; C,c;
1.3.9 Kreissehne
Eine Kreissehne kann durch die beiden Unterklassen Chord und BiChord realisiert werden. Im ersten Fall ist die Sehne definiert durch den Schnitt einer Geraden AB mit einem Kreis k. Im zweiten Fall ist die Sehne bestimmt durch den Schnitt zweier Kreise k1 und k2.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
chord |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Kreis k [C] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
biChord |
< Kreis k1 [C] > , |
||||
| < Kreis k2 [C] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = D; point; dragable; 4.0,2.0; e[5] = k1; circle; radius; A,B; e[6] = k2; circle; radius; C,D; e[7] = s; line; biChord; k1,k2;
1.3.10 Kante / Edge
Ein Edge Objekt ist speziell für die Visualisierung von mathematischen
Graphen ausgelegt.
Es verbindet zwei Vertex-Objekte durch eine Kante und gehört einem
Graph-Objekt an.
Die Darstellung der Kante auf der Zeichenfläche wird durch eine Integer-Variable
int
festgelegt.
Ist int
= 1, so werden die Knotenpunkte durch eine Strecke verbunden.
Ist int
= 2, 3, 4, ... werden die Knotenpunkte durch wechselseitig verlaufende
Kreisbögen dargestellt.
Die Kante wird als Kreis dargestellt, wenn die beiden Knotenpunkte auf
das gleiche Vertex-Objekt verweisen. Die Variable int
bestimmt in diesem Fall den Radius des Kreises, durch den die Kante symbolisiert
wird.
An edge object is developed for the visualisation of mathematical graphs.
An edge connects two vertices and referes to a graph objects, where the
edge object belongs to.
The shape of the edge can be determined by an given integer
int value.
If int
= 1 then the vertices are connected by a line segment.
If int
= 2, 3, 4, ... the edge is shown as an arc on the left or right side.
The edge is shown as a circle, if the two vertices are equal. The variable
int
then determines the radius of the circle.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
edge |
< Vertex [P] > , |
||||
| < Vertex [P] > , | |||||||
| < int [i] > , | |||||||
| < Graph-Object > | |||||||
|
|
|||||||
Beispiel / Example:
e[1] = graph; polygon; graph; "";
e[2] = X1; point; vertex; graph,-5.0,4.0;
e[3] = X2; point; vertex; graph,4.1,-2.75;
e[4] = X3; point; vertex; graph,5.0,4.0;
e[5] = X4; point; vertex; graph,4.1,4.75;
e[6] = a; line; edge; X1,X2,1,graph;
e[7] = b; line; edge; X1,X2,2,graph;
e[8] = c; line; edge; X3,X3,1,graph;
e[9] = d; line; edge; X3,X3,2,graph;
1.4 Kurven / Curves
1.4.1 Parametrisierte Kurven / Parametric curves
Parametrisierte Kurven lassen sich durch
die Unterklasse Curve realisieren. Sie können in kartesischen
Koordinaten in der Form
|
|
Die Funktionen fx ( t ), fy ( t ) und F(t) werden durch Objekte der Klasse MeasureCalculate realisiert, der Kurvenparameter ist darin mit t zu bezeichnen. Ferner ist eine Anzahl n von Stützpunkten anzugeben, durch die die Kurve approximiert wird.
Falls die Kurve nicht in dem Weltkoordinatensystem der Zeichenfläche dargestellt werden soll, kann als Alternative ein Koordinatensystem-Objekt (Seite pageref) angegeben werden.
Parametric curves are implemented by the subclass Curve. They can be
determined by use of euclidian coordinates
|
|
The functions fx ( t ), fy ( t ) und F(t) are implemented by objects of the class MeasureCalculate, the parameter of the curve is to be indicated by t. Additionally, a number of n bases is to be determined, which are used to approximate the curve.
In case the curve is supposed to be displayed in a coordinate system
that is different from the one of the drawing area, as an alternative
a coordinate system object can be (pageref).
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
curve |
< fx ( t ) [MC] > , |
||||
| < fy ( t ) [MC] > , | |||||||
| < t0 [d] > , | |||||||
| < t1 [d] > , | |||||||
| < n [i] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
curve |
< fx ( t ) [MC] > , |
||||
| < fy ( t ) [MC] > , | |||||||
| < Koord.-Syst. [CO] > , | |||||||
| < t0 [d] > , | |||||||
| < t1 [d] > , | |||||||
| < n [i] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
curve |
< F( t ) [MC] > , |
||||
| < t1 [d] > , | |||||||
| < n [i] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
curve |
< F( t ) [MC] > , |
||||
| < Koord.-Syst. [CO] > , | |||||||
| < t1 [d] > , | |||||||
| < n [i] > | |||||||
|
|
|||||||
Beispiel:
e[1] = a; measure; controller; 10.0,10.0,5.0,1.0,"a = ","";
e[2] = b; measure; controller; 10.0,8.0,2.0,1.0,"b = ","";
e[3] = p1; line; curve; "t","calculate(a)*t^2",
-4.0,4.0,50;
e[4] = O; point; fixed; 4.0,4.0;
e[5] = coord; point; coordSystem; O,200,200,200,200;
e[6] = p1; line; curve; "t","calculate(a)*t^2+
calculate(b)*t",coord,
-4.0,4.0,50;
1.4.2 Externe Kurven-Klassen / External classes of curves
Mit Hilfe der Unterklasse Curve lassen sich Kurven einbinden, die durch separate, speziell entwickelte Java-Klassen berechnet werden. Die Objektdaten bestehen dabei aus n Zeichenketten S1, ..., Sn mit 1 £ n £ 10. Vereinbarungsgemäß enthält S1 den Bezeichner der Klasse, die eingebunden werden soll. Die restlichen Zeichenketten können weitere Objektbezeichner oder numerische Werte als Parameter für die Kurvenberechnung enthalten.
By use of the subclass Curve it is possible to implement curves, which can be generated by separate, specially developed Java-classes. Its object data ist composed of n strings S1, ..., Sn where 1 £ n £ 10. S1 will be given the object label of the class, into which it is to be implemented. The remaining strings may have additional object labels or numeric values as parameters for the genration of the curve.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
curve |
< S1 [s] > , |
||||
| < ... > , | |||||||
| < Sn [s] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; -5.0,0.0; e[2] = B; point; dragable; 5.0,0.0; e[3] = s; measure; controller; 10.0,11.0,1.0,3.0,"",""; e[4] = k; line; curve; "Kochkurve","A","B","s";
1.4.3 Ortslinie / Locus
Mit Hilfe der Unterklasse Locus lassen sich Ortslinien abhängiger Punkte realisieren. Als Objektdaten müssen dazu zwei Punkte O und M sowie eine Führungslinie k angegeben werden. Wird M nun entlang von k bewegt, so approximiert die zu erzeugende Ortslinie die Bahn von O mit n Stützpunkten.Als Führungslinie können die geometrischen Objekte Gerade, Kreis, Ortslinie oder Kurve dienen. Handelt es sich bei der Führungslinie um eine Ortslinie oder um eine Kurve, so braucht diese nicht explizit bei den Objektdaten angegeben zu werden. Sie wird als Bezugsobjekt von M automatisch erkannt.
The subclass Locus implements loci of dependent points. The two points O and M and a line of guidance k have to be determined. When M is dragged along the line k, the resulting locus approximates the course of O with n base points.
The geometric objects straight line, circle, locus, or can be used as
a line of guidance. In case, the line of guidance is a locus or a curve,
it is not necessary to explicitly designate this with the object data.
It will be recognized automatically as M’s point of reference.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
locus |
< Punkt O [P] > , |
||||
| < Punkt M [P] > , | |||||||
| < Gerade k [L] > , | |||||||
| < Stützpkte. n [i] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
locus |
< Punkt O [P] > , |
||||
| < Punkt M [P] > , | |||||||
| < Kreis k [C] > , | |||||||
| < Stützpkte. n [i] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
locus |
< Punkt O [P] > , |
||||
| < Punkt M [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; -5.0,0.0; e[2] = B; point; dragable; -7.13,5.2; e[3] = C; point; dragable; 10.13,7.93; e[4] = s1; line; connect; A,B; e[5] = s2; line; connect; C,B; e[6] = P1; point; dragable; -9.89,-2.58,s1; e[7] = P2; point; proportion; A,B,A,P1,B,C,B,C; e[8] = s3; line; connect; P1,P2; e[9] = P3; point; proportion; A,B,A,P1,P1,P2,P1,P2; e[10] = l; line; locus; P3,P1,s1,50;
1.4.4 Kegelschnitte
Kegelschnitte können mit Hilfe der Klasse Conic durch vier alternative Definitionsformen erzeugt werden:- durch die Angabe des Parameters p, der linearen Exzentrizität e sowie
eines Drehwinkels a und einer Verschiebung um vx und vy,
- durch die Angabe von a2 und b2 als Achsenabschnitte,
- durch die Angabe der Parameter A, B, C, D, E, F der allgemeinen Kegelschnittgleichung
und
- durch die Angabe von fünf Punkten, durch die der Kegelschnitt verlaufen
soll.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
conic |
< Parameter p [M] > , |
||||
| < Exzentr. e [M] > , | |||||||
| < Winkel a [M] > , | |||||||
| < Transl. vx [M] > , | |||||||
| < Transl. vy [M] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
conic |
< Achsenabs. a2 [M] > , |
||||
| < Achsenabs. b2 [M] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
conic |
< Parameter A [M] > , |
||||
| < Parameter B [M] > , | |||||||
| < Parameter C [M] > , | |||||||
| < Parameter D [M] > , | |||||||
| < Parameter E [M] > , | |||||||
| < Parameter F [M] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
conic |
< Punkt [P] > , |
||||
| < Punkt [P] > , | |||||||
| < Punkt [P] > , | |||||||
| < Punkt [P] > , | |||||||
| < Punkt [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,7.0; e[2] = B; point; dragable; -5.0,1.0; e[3] = C; point; dragable; 3.0,6.0; e[4] = D; point; dragable; 5.0,0.0; e[5] = E; point; dragable; -4.0,4.0; e[6] = c; line; conic; A,B,C,D,E;
1.5 Kreise / Circles
1.5.1 Kreis / Circle
Ein Kreis wird durch die beiden Unterklassen Radius und CircumCircle realisiert. Im ersten Fall wird der Kreis definiert durch die Angabe eines Mittelpunkts M und den Radius r. Der Radius r kann dabei auf drei Arten festgelegt werden:- durch einen Punkt P mit r=|MP|,
- durch zwei Punkte P1P2 mit r = |P1P2| oder
- durch eine Strecke AB mit r=|AB|.
Im zweiten Fall wird der Kreis definiert durch die Angabe von drei Punkten ABC, die auf der Kreislinie liegen.
A circle is implemented in the subclasses Radius and CircumCircle. In the former case, the circle is defined by a midpoint M and the radius r. The radius r can be determined in three different ways:
- by a point P where r = |MP|,
- by two points P1P2 where r = |P1P2|
or
- by a line segment AB where r = |AB|.
If CircumCircle is used the circle is defined by determining three points ABC, which are located on the line of the circle.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
circle |
radius |
< Punkt M [P] > , |
||||
| < Punkt P [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
circle |
radius |
< Punkt M [P] > , |
||||
| < Punkt P1 [P] > , | |||||||
| < Punkt P2 [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
circle |
radius |
< Punkt M [P] > , |
||||
| < Strecke AB [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
circle |
circumCircle |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = D; point; dragable; 4.0,2.0; e[5] = k1; circle; radius; A,B; e[6] = k2; circle; circumCircle; A,C,D;
1.5.2 Inversion eines Kreises an einem Kreis
Durch die Inversion eines Kreises an einem Kreis wird wiederum ein Kreis erzeugt. Dieses läßt sich durch die Unterklasse Invert realisieren. Als Objektdaten sind zwei Kreise k1 und k2 anzugeben.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
circle |
invert |
< Kreis k1 [C] > , |
||||
| < Kreis k2 [C] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = D; point; dragable; 4.0,2.0; e[5] = k1; circle; radius; A,B; e[6] = k2; circle; radius; C,D; e[7] = k3; circle; invert; k1,k2;
1.6 Kreissektoren / Sectors of Circles
1.6.1 Kreisbogen / Arc of circle
Mit Hilfe der Unterklassen Sector und Arc können Kreisbogen erzeugt werden. Im ersten Fall ist dazu ein Winkel ÐABC durch drei Punkte anzugeben, wobei der Kreisbogen mit dem Kreismittelpunkt B und dem Radius AB von A aus in Richtung auf C verläuft.Im zweiten Fall wird ein Kreisbogen durch die Angabe von drei Punkten ABC auf der Kreislinie definiert. Der Bogen wird dabei durch die Punkte A und C begrenzt.
The subclasses Sector and Arc can be used to generate arcs of circles. When using the subclass Sector the angle ÐABC which is determined by three points has to be provided. The arc of the circle, that has its midpoint in B and a radius of AB, starts in A and continues towards C.
When using the subclass Arc the arc of the circle is defined by providing
three points ABC on the course of the circle. The arcs ends are determined
by the points A and C.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
sector |
sector |
< Punkt B [P] > , |
||||
| < Punkt A [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
sector |
arc |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = s; sector; sector; B,A,C; e[5] = a; sector; arc; A,B,C;
1.6.2 Winkelbogen / Arc of angle
Mit Hilfe der Unterklasse Angle kann ein Winkelbogen erzeugt werden. Der Winkel ÐABC wird dabei durch drei Punkte definiert. Durch die optionale Angabe zweier Zeichenketten s1 und s2 kann die Winkelgröße berechnet und ihr Wert auf der Zeichenfläche ausgegeben werden. Dabei werden s1 und s2 vor und hinter der Winkelgröße angezeigt.
The subclass Angle implements arcs of angles. The angle ÐABC is defined by three points. Optionally two strings s1 and s2 can be determined making it possible to calculate the degree of the angle and to have it displayed in the drawing area. s1 and s2 will then be displayed in front of and behind the degree of the angle.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
sector |
angle |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
sector |
angle |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < Präfix s1 [s] > , | |||||||
| < Postfix s2 [s] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = s; sector; angle; A,B,C,"\beta = "," °";
1.7 Polygone / Polygons
1.7.1 Polygon mit vorgegebenen Eckpunkten / Polygons with predetermined number of vertices
Aus einer vorgegebenen Anzahl von Eckpunkten kann durch die Unterklasse Polygon ein Vieleck realisiert werden. Als Objektdaten sind dazu n Eckpunkte P1, ¼, Pn anzugeben, mit 3 £ n £ 17.
For a given number of vertices the subclass Polygon can generate a polygon. The object data needed are the vertices P1, ¼, Pn, where 3 £ n £ 17.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
polygon |
polygon |
< Punkt P1 [P] > , |
||||
| ..., | |||||||
| < Punkt Pn [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = C; point; dragable; 4.0,0.0; e[4] = D; point; dragable; 4.0,2.0; e[5] = p; polygon; polygon; A,B,C,D;
1.7.2 Gleichseitiges Dreieck
Gleichseitige Dreiecke werden durch die Unterklasse EquilateralTriangle realisiert. Als Objektdaten sind dazu zwei Eckpunkte A und B anzugeben, die die Seitenlänge festlegen.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
polygon |
equilateralTriangle |
< Punkt A [P] > , |
||||
| < Punkt B [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,1.0; e[2] = B; point; dragable; 0.0,0.0; e[3] = p; polygon; equilateralTriangle; A,B;
1.7.3 Ähnliches Dreieck
Ähnliche Dreiecke lassen sich durch die Unterklasse Similar realisieren. Als Objektdaten sind dazu ein Dreieck ABC und zwei Eckpunkte D und E anzugeben.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
polygon |
similar |
< Punkt D [P] > , |
||||
| < Punkt E [P] > , | |||||||
| < Punkt A [P] > , | |||||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; -6.0,5.0; e[2] = B; point; dragable; -3.0,5.0; e[3] = C; point; dragable; -5.0,0.0; e[4] = D; point; dragable; 0.0,5.0; e[5] = E; point; dragable; 3.0,5.0; e[6] = p; polygon; similar; D,E,A,B,C;
1.7.4 Quadrat
Quadrate lassen sich durch die Unterklasse Square realisieren. Dabei muß eine Quadratseite durch zwei Punkte AB angegeben werden.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
polygon |
square |
< Punkt A [P] > , |
||||
| < Punkt B [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; -6.0,5.0; e[2] = B; point; dragable; -3.0,5.0; e[3] = p; polygon; square; A,B;
1.7.5 Parallelogramm
Zu drei Punkten A, B, C kann mit Hilfe der Unterklasse Parallelogram ein Kantenzug erzeugt werden, der ein Parallelogramm darstellt.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
polygon |
parallelogram |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; -6.0,5.0; e[2] = B; point; dragable; -3.0,5.0; e[3] = C; point; dragable; 3.0,0.0; e[4] = p; polygon; parallelogram; A,B,C;
1.7.6 Reguläre Polygone
Aus einer Seite AB heraus kann man mit Hilfe der Unterklasse RegularPolygon ein regelmäßiges n-Eck erzeugen.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
polygon |
regularPolygon |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < n [i] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 6.0,5.0; e[2] = B; point; dragable; 3.0,5.0; e[3] = p; polygon; regularPolygon; A,B,5;
1.7.7 Reguläre Sternpolygone
Aus einer Seite AB heraus kann man mit Hilfe der Unterklasse starPolygon ein regelmäßiges, sternförmiges n-Eck erzeugen, das eine Kante zwischen jeder i-ten Ecke hat.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
polygon |
starPolygon |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < n [i] > , | |||||||
| < i [i] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 6.0,5.0; e[2] = B; point; dragable; 3.0,5.0; e[3] = p; polygon; starPolygon; A,B,5,3;
1.7.8 Graphen / Graphs
Ein Graph Objekt ist speziell für die Visualisierung von mathematischen Graphen ausgelegt.Das Objekt selbst ist abstrakt, dass heisst, es benötigt keine Konstruktionsparameter.
Sobald jedoch Eckpunkte (Vertex-Objekte) oder Kanten (Edge-Objekte) konstruiert werden,
erstellt das Graph-Objekt eine Matrix des Graphen.
Mit Hilfe des JavaScript-Befehls document.Geometria.getPropertyString("graph","matrix")
kann die Matrix abgerufen werden.
Ferner besitzt ein Graph-Objekt die Eigenschaften: numVertices,
numEdges
und isConnected.
A graph object can be used for the visualisation of mathmatical graphs.
The object itself is abstract, that means, there is no parameter data
needed.
If an edge object or a vertex object is constructed, the graph object
recognizes this
and builts a matrix of the graph.
With the help of the JavaScript command document.Geometria.getPropertyString("graph","matrix")
the matrix can be transfert to an HTML-page.
Other properties, which are for graph objects available, are: numVertices,
numEdges
and isConnected.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
polygon |
graph |
""; |
||||
|
|
|||||||
Beispiel:
e[1] = graph; polygon; graph; "";
e[2] = X1; point; vertex; graph,-5.0,4.0;
e[3] = X2; point; vertex; graph,4.1,-2.75;
e[4] = X3; point; vertex; graph,5.0,4.0;
e[5] = X4; point; vertex; graph,4.1,4.75;
e[6] = a; line; edge; X1,X2,1,graph;
e[7] = m0; measure; property; graph,"isConnected",20,20,"","";
e[8] = m1; measure; property; graph,"numVertices",20,40,"","";
e[9] = m2; measure; property; graph,"numEdges",20,60,"","";
1.8 Punktmengen
Mit Hilfe der Unterklasse PointSet kann eine statische Punktmenge auf der Zeichenfläche erzeugt werden. Dazu ist die Angabe einer Bilddatei erforderlich. Die Menge aller schwarz gefärbten Bildpunkte definiert die Punktmenge. Als optionaler Parameter n kann die Größe des Arrays zum Speichern der Punktmenge begrenzt werden. Hierdurch wird Speicherplatz gespart. Wenn die Punktmenge als Bezugsobjekt für einen ziehbaren Punkt dient, kann zwischen zwei alternativen Verfahren im Zugmodus gewählt werden. Voreingestellt ist der ''Gummibandmodus'', d. h. ein ziehbarer Punkt kann wie an einem Gummiband innerhalb der Punktmenge gezogen werden. Wird ein dritter Parameter i angegeben, so ist der ''Gummibandmodus'' ausgeschaltet und ein Punkt läßt sich mit bis zu i Bildschirmpunkten Abstand zum Mauszeiger ziehen.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
line |
pointSet |
< Dateiname [s] > |
||||
|
|
|||||||
|
< Name [s] > |
line |
pointSet |
< Dateiname [s] > , |
||||
| < n [i] > | |||||||
|
|
|||||||
|
< Name [s] > |
line |
pointSet |
< Dateiname [s] > , |
||||
| < n [i] > , | |||||||
| < i [i] > | |||||||
|
|
|||||||
Beispiel:
e[1] = Pset; line; pointSet; "Kurve01.gif", 10000, 10; e[2] = A; point; dragable; 2.7,5.4, Pset;
1.9 Koordinatensysteme / Coordinate Systems
Mit Hilfe der Unterklasse CoordSystem kann ein Koordinatensystem auf der Zeichenfläche erzeugt werden, in dem Kurven oder Punkte dargestellt werden können. Die Längen der Koordinatenachsen werden in Bildschirmpunkten durch die vier Variablen v1 (negative x-Achse), v2 (positive x-Achse), v3 (negative y-Achse) und v4 (positive y-Achse) festgelegt. Die Größe der x- und y-Einheit wird durch den Wert zweier Funktionale oder durch den Abstand von jeweils zwei Punkten, mit dx = |P1P2| und dx = |P3P4|, bestimmt.
The subclass CoordSystem makes it possible to generate a coordinate system that can display curves or points in the drawing area. The length of the axes of the coordinate system are determined in pixel. For that purpose the four v1 (negative x-axis), v2 (positive x-axis), v3 (negative y-axis), and v4 (positive y-axis) are to be provided. The size of the x- and y-unit is determined by the value of a function or by the distance of two points each with dx = |P1P2| and dx = |P3P4|.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
point |
coordSystem |
< Ursprung [P] > , |
||||
| < x-Einheit [M] > , | |||||||
| < y-Einheit [M] > , | |||||||
| < v1 [i] > , | |||||||
| < v2 [i] > , | |||||||
| < v3 [i] > , | |||||||
| < v4 [i] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
coordSystem |
< Ursprung [P] > , |
||||
| < P1 [P] > , | |||||||
| < P2 [P] > , | |||||||
| < P3 [P] > , | |||||||
| < P4 [P] > , | |||||||
| < v1 [i] > , | |||||||
| < v2 [i] > , | |||||||
| < v3 [i] > , | |||||||
| < v4 [i] > | |||||||
|
|
|||||||
|
< Name [s] > |
point |
coordSystem |
< Ursprung [P] > , |
||||
| < v1 [i] > , | |||||||
| < v2 [i] > , | |||||||
| < v3 [i] > , | |||||||
| < v4 [i] > | |||||||
|
|
|||||||
Beispiel:
e[1] = O; point; dragable; -6.0,-6.0; e[2] = X; point; dragable; 6.0,-6.0; e[3] = Y; point; dragable; 6.0,0.0; e[4] = c; point; coordSystem; O,X,Y,X,Y,200,200,200,200;
Chapter 2
Funktionale / Functions
2.1 Hinweise zum Arbeiten mit Funktionalen
Im folgenden sollen einige Hinweise zum Arbeiten mit Funktionalen gegeben werden. Unter einem Funktional wird in diesem Zusammenhang eine Abbildung F\colon M ® \R verstanden. Der Definitionsbereich M besteht dabei aus dem Zustandsraum einer Menge von Objekten. Der Wert eines Funktionals ist eine reelle Zahl. Durch Funktionale können die Eigenschaften von Objekten gemessen werden und es lassen sich Relationen zwischen mehreren Objekten prüfen. Funktionale haben mehrere Aufgaben:- Sie liefern Parameterwerte für die Konstruktion geometrischer Objekte.
- Sie werden bei der Definition von Antwortwerten und Prüfschlüsseln
für eine Antwortanalyse verwendet.
- Sie geben Rückmeldung über den Figurenzustand an den Schüler, indem
die Werte auf der Zeichenfläche angezeigt werden.
2.2 Eigenschaften von Objekten / Object Properties
2.2.1 Eigenschaften von Punktobjekten / Properties of Points
Mit Hilfe der Unterklasse Property kann auf die Eigenschaften eines Punkts zugegriffen werden. Neben den x- und y-Koordinaten kann mit defined geprüft werden, ob die Koordinaten reelle Werte enthalten. Ist der Punkt ziehbar auf einer parametrisierten Kurve, so kann der Wert des Kurvenparameters t gemessen werden.
The subclass Property makes it possible to access the properties of points. Next to the x- and y-coordinats the property defined can be used to check whether the coordinates are real numbers. If the point is dragable along a parametric curve, the value of the curve’s parameter t can be measured.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Punkt [P] > , |
||||
| < x-Koordinate ["x"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Punkt [P] > , |
||||
| < y-Koordinate ["y"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Punkt [P] > , |
||||
| < Koord. reell? ["defined"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Punkt [P] > , |
||||
| < Kurvenparameter ["t"] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 2.0,5.0; e[2] = m0; measure; property; A,"x",10.0,5.0,"A.x = ",""; e[3] = m1; measure; property; A,"y",10.0,4.0,"A.y = ",""; e[4] = m2; measure; property; A,"defined";
2.2.2 Eigenschaften von Strecken und Geraden / Properties of line segments and straight lines
Auf die Eigenschaften von Strecken und Geraden kann durch die Unterklasse Property zugegriffen werden.
The properties of line segments and straight lines can be accessed with the subclass Property.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Gerade [L] > , |
||||
| < Steigung ["slope"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Gerade [L] > , |
||||
| < Abstand ["distance"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Gerade [L] > , |
||||
| < ax + by + c = 0 ["Param_a"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Gerade [L] > , |
||||
| < ax + by + c = 0 ["Param_b"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Gerade [L] > , |
||||
| < ax + by + c = 0 ["Param_c"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Gerade [L] > , |
||||
| < y = mx + b ["b"] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 2.0,5.0;
e[2] = B; point; dragable; 1.0,0.0;
e[3] = g; line; straightLine; A,B;
e[4] = m0; measure; property; g,"slope",10.0,10.0,
"Steigung = ","";
2.2.3 Eigenschaften von Kreisen / Properties of circles
Mit Hilfe der Unterklasse Property kann auf die Eigenschaften von Kreisen zugegriffen werden.
The subclass Property makes it possible to access the properties of circles.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Kreis [C] > , |
||||
| < (x - x0)2 + (y - y0)2 = r2 ["x0"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Kreis [C] > , |
||||
| < (x - x0)2 + (y - y0)2 = r2 ["y0"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Kreis [C] > , |
||||
| < (x-x0)2+(y-y0)2=r2 ["r2"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Kreis [C] > , |
||||
| < Radius ["radius"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Kreis [C] > , |
||||
| < Durchmesser ["perimeter"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Kreis [C] > , |
||||
| < Flächeninhalt ["area"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Kreis [C] > , |
||||
| < Umfang ["circumference"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Kreis [C] > , |
||||
| < x-Koordinate des Mittelpunkts ["center_x"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Kreis [C] > , |
||||
| < y-Koordinate des Mittelpunkts ["center_y"] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 2.0,5.0;
e[2] = B; point; dragable; 1.0,0.0;
e[3] = k; circle; radius; A,B;
e[4] = m0; measure; property; k,"area",8.0,10.0,
"Flächeninhalt = "," F.E.";
e[5] = m1; measure; property; k,"circumference",8.0,9.0,
"Umfang = "," L.E.";
2.2.4 Eigenschaften von Polygonen / Properties of Polygons
Mit Hilfe der Unterklasse Property kann auf die Eigenschaften von Polygonen zugegriffen werden.
The subclass Property implements access to the properties of polygons.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Flächeninhalt ["area"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Umfang ["circumference"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Anzahl von Symmetrieachsen ["numSymmetryAxis"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Anzahl von Drehsymmetrien ["numSymmetryRotation"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Konvexität ["isConvex"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Regularität ["isRegular"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Affine Regularität ["isAffinRegular"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Anz. inzidierender Eckpunkte ["numIncidentVertex"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Umfang ["circumference"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < x-Koordinate des Mittelpunkts ["center_x"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < y-Koordinate des Mittelpunkts ["center_y"] > | |||||||
|
|
|||||||
Falls das Polygon ein Dreieck ist, können die besonderen Dreiecksklassen analysiert werden. Der Befehl bestClass liefert die beste Dreiecksklasse. Mit dem Befehl checkClass_i kann ein vorliegendes Dreieck gezielt auf eine bestimmte Klasse hin geprüft werden.
If the polygon is a triangle, the polygon can be analysed to fit a special class of triangles. The command bestClass determines which class fits best. The command checkClass_i can be used to check whether a given triangle belongs to a certain class.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < beste Figurenklasse ["bestClass"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < gleichseitig ["checkClass_1"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < gleichschenklig u. rechtwinklig ["checkClass_2"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < gleichschenklig u. stumpfwinklig ["checkClass_3"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < gleichschenklig u. spitzwinklig ["checkClass_4"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < rechtwinklig ["checkClass_5"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < stumpfwinklig ["checkClass_6"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < spitzwinklig ["checkClass_7"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < gleichschenklig ["checkClass_8"] > | |||||||
|
|
|||||||
Falls das Polygon ein Viereck ist, können die besonderen Vierecksklassen erkannt werden. Der Befehl bestClass liefert die beste Vierecksklasse. Mit dem Befehl checkClass_i kann ein vorliegendes Viereck gezielt auf eine bestimmte Klasse hin geprüft werden.
If the polygon is a quadrangle, special cases of quadrangles can be recognized. The command bestClass can be used to determine which quadrangle class fits best. The command checkClass_i can be used to check whether a given quadrangle matches with a certain class.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < beste Figurenklasse ["bestClass"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Quadrat ["checkClass_1"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Rechteck ["checkClass_2"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Raute ["checkClass_3"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Parallelogramm ["checkClass_4"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < gleichschenkliges Trapez ["checkClass_5"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < schiefes Trapez ["checkClass_6"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < gleichschenkliger Drachen ["checkClass_7"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < schiefer Drachen ["checkClass_8"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < schräger Drachen ["checkClass_9"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Sehnenviereck ["checkClass_10"] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
property |
< Polygon [PG] > , |
||||
| < Pythagoräisches Viereck ["checkClass_11"] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 2.0,5.0;
e[2] = B; point; dragable; 1.0,0.0;
e[3] = C; point; dragable; 2.0,1.0;
e[4] = D; point; dragable; 1.0,4.0;
e[5] = p; polygon; polygon; A,B,C,D;
e[6] = m0; measure; property; p,"area",8.0,10.0,
"Flächeninhalt = "," F.E.";
e[7] = m1; measure; property; p,"circumference",8.0,9.0,
"Umfang = "," L.E.";
e[8] = m2; measure; property; p,"bestClass";
2.3 Implementierte Funktionale
2.3.1 Abstand
Durch die Unterklasse Distance kann der euklidische Abstand zwischen zwei Objekten gemessen werden.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
distance |
< Punkt [P] > , |
||||
| < Punkt [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
distance |
< Punkt [P] > , |
||||
| < Gerade [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
distance |
< Punkt [P] > , |
||||
| < Kreis [C] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 2.0,5.0;
e[2] = B; point; dragable; 1.0,0.0;
e[3] = C; point; dragable; 2.0,1.0;
e[4] = g; line; straightLine; A,B;
e[5] = m0; measure; distance; C,g,8.0,10.0,
"Abstand = "," L.E.";
2.3.2 Winkel
Durch die Unterklasse Angle kann ein durch drei Punkte definierter Winkel ÐABC gemessen werden.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
angle |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 2.0,5.0;
e[2] = B; point; dragable; 1.0,0.0;
e[3] = C; point; dragable; 2.0,1.0;
e[4] = m0; measure; angle; A,B,C,8.0,10.0,
"Winkel = "," °";
2.3.3 Streckenverhältnisse
Durch die Unterklasse Ratio kann das Verhältnis einer Strecke AB zu einer Strecke CD gemessen werden.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
ratio |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < Punkt D [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 2.0,5.0;
e[2] = B; point; dragable; 1.0,0.0;
e[3] = C; point; dragable; 2.0,1.0;
e[4] = D; point; dragable; 2.0,3.0;
e[5] = m0; measure; ratio; A,B,C,D,8.0,10.0,
"AB/CD = ","";
2.3.4 Ähnlichkeit
Durch die Unterklasse Similarity kann geprüft werden, ob zwei Polygone zueinander ähnlich sind. Das Funktional liefert den Wert 1 oder 0.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
similarity |
< Polygon [PG] > , |
||||
| < Polygon [PG] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 2.0,5.0;
e[2] = B; point; dragable; 1.0,0.0;
e[3] = C; point; dragable; 2.0,1.0;
e[4] = D; point; dragable; 2.0,3.0;
e[5] = E; point; dragable; 6.0,2.0;
e[6] = F; point; dragable; 7.0,3.0;
e[7] = d1; polygon; polygon; A,B,C;
e[8] = d2; polygon; polygon; D,E,F;
e[9] = m0; measure; similarity; d1,d2,8.0,10.0,
"d1 ~ d2 = ","";
2.3.5 Kollinearität
Mit Hilfe der Unterklasse Collinear kann geprüft werden, ob drei Punkte zueinander kollinear sind. Das Funktional liefert den Wert 1 oder 0.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
collinear |
< Punkt [P] > , |
||||
| < Punkt [P] > , | |||||||
| < Punkt [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 2.0,5.0;
e[2] = B; point; dragable; 1.0,0.0;
e[3] = C; point; dragable; 2.0,1.0;
e[4] = m0; measure; collinear; A,B,C,8.0,10.0,
"Kollinearität = ","";
2.3.6 Kongruenz
Mit Hilfe der Unterklasse Congruence kann geprüft werden, ob zwei Polygone oder zwei Kreise kongruent sind. Das Funktional liefert den Wert 1 oder 0.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
congruence |
< Polygon [PG] > , |
||||
| < Polygon [PG] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
congruence |
< Kreis [C] > , |
||||
| < Kreis [C] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0;
e[2] = B; point; dragable; 0.0,4.0;
e[3] = k1; circle; radius; A,B;
e[4] = C; point; dragable; 2.0,3.0;
e[5] = D; point; dragable; 2.0,4.0;
e[6] = k2; circle; radius; C,D;
e[7] = m0; measure; congruence; k1,k2,8.0,10.0,
"Kongruenz = ","";
2.3.7 Inzidenz
Mit Hilfe der Unterklasse Incidence kann geprüft werden, ob ein Punkt P mit einem Objekt O inzidiert. Das Funktional liefert den Wert 1 oder 0.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
incidence |
< Punkt P [P] > , |
||||
| < Punkt O [P] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
incidence |
< Punkt P [P] > , |
||||
| < Gerade O [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
incidence |
< Punkt P [P] > , |
||||
| < Kreis O [C] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
incidence |
< Punkt P [P] > , |
||||
| < x-Koordinatenfkt. [M] > , | |||||||
| < y-Koordinatenfkt. [M] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0;
e[2] = B; point; dragable; 0.0,4.0;
e[3] = k; circle; radius; A,B;
e[4] = P; point; dragable; 2.0,4.0;
e[5] = m0; measure; incidence; P,k,8.0,10.0,
"P liegt auf k = ","";
2.3.8 Inklusion
Mit Hilfe der Unterklasse Inclusion kann geprüft werden, ob sich ein Punkt innerhalb der Fläche eines Kreises oder eines Polygons befindet. Das Funktional liefert den Wert 1 oder 0.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
inclusion |
< Punkt [P] > , |
||||
| < Kreis [C] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
inclusion |
< Punkt [P] > , |
||||
| < Polygon [PG] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0;
e[2] = B; point; dragable; 0.0,4.0;
e[3] = k; circle; radius; A,B;
e[4] = P; point; dragable; 2.0,4.0;
e[5] = m0; measure; inclusion; P,k,8.0,10.0,
"P liegt in k = ","";
2.3.9 Parallelität
Mit Hilfe der Unterklasse Parallel kann geprüft werden, ob zwei Geraden AB und CD zueinander parallel sind. Das Funktional liefert den Wert 1 oder 0.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
parallel |
< Gerade AB [L] > , |
||||
| < Gerade CD [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
parallel |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < Punkt D [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0;
e[2] = B; point; dragable; 0.0,4.0;
e[3] = C; point; dragable; 3.0,3.0;
e[4] = D; point; dragable; 3.0,4.0;
e[5] = g; line; straightLine; A,B;
e[6] = h; line; straightLine; C,D;
e[7] = m0; measure; parallel; g,h,8.0,10.0,
"g || h = ","";
2.3.10 Orthogonalität
Durch die Unterklasse Perpendicular kann geprüft werden, ob zwei Geraden AB und CD zueinander orthogonal sind. Das Funktional liefert den Wert 1 oder 0.|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
perpendicular |
< Gerade AB [L] > , |
||||
| < Gerade CD [L] > | |||||||
|
|
|||||||
|
< Name [s] > |
measure |
perpendicular |
< Punkt A [P] > , |
||||
| < Punkt B [P] > , | |||||||
| < Punkt C [P] > , | |||||||
| < Punkt D [P] > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0;
e[2] = B; point; dragable; 0.0,4.0;
e[3] = C; point; dragable; 3.0,3.0;
e[4] = D; point; dragable; 3.0,4.0;
e[5] = g; line; straightLine; A,B;
e[6] = h; line; straightLine; C,D;
e[7] = m0; measure; perpendicular; g,h,8.0,10.0,
"g orthogonal zu h = ","";
2.4 Umgang mit Termen / Working
with Terms
2.4.1 Termevaluation / Term evaluation
Das Berechnen von Termen erfolgt durch die Unterklasse Calculate. Ein Term wird als Zeichenkette in Anführungszeichen angegeben. In dem Term können die mathematischen Operatoren + - * / ^ enthalten sein. Daneben gibt es die logischen Verknüpfungen UND (&), ODER ( | ) und XOR (**). Die Negation ist als Funktion not() realisiert. Weitere verfügbare mathematische Funktionen sind: sin(), cos(), tan(), sqrt(), min(), max(), asin(), acos(), atan(), exp(), log() und abs().In einem Term gibt es außerdem mehrere alternative Möglichkeiten, Funktionale einzubinden.
- Um auf ein bereits im Skript definiertes Funktional Bezug zu nehmen,
kann der Befehl calculate( < Objektbezeichner > )
verwendet werden.
- Um auf die Eigenschaften von Objekten zuzugreifen, steht der Befehl
$( < Objektbezeichner > , < Objekteigenschaft
> ) zur Verfügung. Die Objekteigenschaften entsprechen dabei
den in Abschnitt ''Eigenschaften von Objekten'' (Seite pageref-pageref)
aufgeführten Parametern.
- Um die in GeoScript implementierten Funktionale zu verwenden,
sind die folgenden Befehle verfügbar: angle(), area(),
isIncident(),
isParallel(), isPerpendicular(), isCollinear(), isIncluded(),
distance(), XVector(), YVector() und isSimilar(). In die Klammern sind jeweils die entsprechenden Parameter einzusetzen (Seite pageref-pageref). - Um speziell auf die Koordinaten eines Punkts zuzugreifen, gibt es alternativ zu dem $()-Befehl die beiden Funktionale coordinateX( < Punktbezeichner > ) und coordinateY( < Punktbezeichner > ).
Terms can be calculated with the subclass Calculate. Terms have to be put in quotation marks. Within ther terms the mathematical operators + - * / ^ may be included. Additionally the logic links AND (&), OR ( | ) and XOR (**) may be included. The negation has been realized as the function not(). Additional included mathematical functions are: sin(), cos(), tan(), sqrt(), min(), max(), asin(), acos(), atan(), exp(), log() and abs().
Inside a term it is possible to include functions several different ways.
- In order to use a function that has previously been defined in the skript, the command calculate( < object label of object > ) can be used.
- In order to access properties of objects, the command $( < object label of object > , < object property > ) can be used. The properties of the objects correspond to the parameters that were described in ''Properties of Objects'' (Seite pageref-pageref) .
- To use the functions that are implemented in GeoScript, the following commands are available: angle(), area(), isIncident(), isParallel(), isPerpendicular(), isCollinear(), isIncluded(), distance(), XVector(), YVector() and isSimilar().The corresponding parameters are to be placed inside the parentheses (pp. pageref-pageref).
- To directly access the coordinates of a point, there is an alternative to the command $()- the two functions coordinateX( < object label of point > ) and coordinateY( < object label of point> ).
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
calculate |
< Term [MC] > |
||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0;
e[2] = B; point; dragable; 3.0,3.0;
e[3] = Mx; measure; calculate; "($(A,x)+$(B,x))/2";
e[4] = My; measure; calculate; "(coordinateY(A)+
coordinateY(B))/2";
e[5] = M; point; functionDepend; "calculate(Mx)",
"calculate(My)";
2.4.2 Prüffunktionen / Functions with boolean values
Mit Hilfe der oben aufgeführten Termevaluation lassen sich auch sog. Prüffunktionen realisieren, die nur die Werte 1 (wahr) und 0 (falsch) annehmen können. Eine Prüffunktionen wird aufgestellt, indem zwei einzelne Terme T1 und T2 (Objekte der Klasse MeasureCalculate) durch die Symbole <, >, = und != verknüpft werden.Bei der Formulierung einer Prüffunktion in einem Skript ist zu beachten, daß T1 und T2 und das Relationssymbol jeweils durch ein Leerzeichen getrennt sind. Innerhalb der Zeichenketten von T1 und T2 dürfen keine Leerzeichen stehen.
Alternativ kann eine Prüffunktion auch durch die Angabe lediglich eines Funktionals definiert werden, sofern sichergestellt ist, daß das Funktional nur die Werte 1 und 0 annehmen kann. Dies ist etwa bei den Funktionalen zum Prüfen auf Ähnlichkeit, Kollinearität, Kongruenz, Inzidenz, Inklusion, Parallelität und Orthogonalität der Fall. Auch läßt sich das Interaktionselement Checkbox als ein booleschwertiges Funktional auffassen.
Verwendet werden Prüffunktionen im Zusammenhang mit Fallunterscheidungen in Termen (Seite pageref), beim Begrenzen des Zustandsraums einer Figur (Seite pageref), beim Ein- und Ausblenden von Objekten (Seite pageref), beim Erzeugen von speziellen Figurenzuständen (Seite pageref) sowie bei der Definition einer Antwortanalyse (Seite pageref) vor.
Eine Prüffunktion als ein separates Objekt zu erzeugen, ist nicht vorgesehen. Daher ist an dieser Stelle auch keine Datentabelle und kein Beispiel aufgeführt.
Using the upper described term evaluation it is possible to implement the so called check-functions, that only deliver values of 1 (true) and 0 (false). A check-function is composed of two single terms T1 and T2 (objects of the class MeasureCalculate) connected with the symbols <, >, = and !=.
When composing a check-function in a skript, it is necessary to put a space each between T1 and T2 and the symbol designating their connection symbol. Within the string T1 and T2 there must not be a space.
As an alternativ the check-function can be definded using only one function if it is asured that this function can only deliver a value of 1 and 0. This is the case with the functions that test for similarity, collinearity, congruency, incidence, inclusion, parallelism, and perpendicularity. The interactional element checkbox can also be seen as a boolean function.
Check-functions are used in the context of case destinctions in terms (page pageref), restricting the area of a figur (page pageref), blending objects in or out (page pageref), generating special states of figures (page pageref) and when a the analysis of an answer is defined (page pageref).
It is not intended to have a check-function generated as a seperate object. Therefore, we have inserted no data table nor examples to this topic.
2.4.3 Terme mit Fallunterscheidungen / Terms with case distinctions
Fallunterscheidungen können mit Hilfe einer Prüffunktion (Seite pageref) realisiert werden. Dazu wird ähnlich wie bei der Definition eines Terms der Unterklasse Calculate vorgegangen. Der Term muß jedoch wie folgt aufgebaut sein: "if ( < Prüffkt. [MCond] > ) then ( < Term [MC] > ) else ( < Term [MC] > )".
Case distinctions can be implemented by a check-function (page pageref) . The procedure is similar to defining a term for the subclass Calculate. But the term has to be of the form: "if ( < probefunction [MCond] > ) then ( < term [MC] > ) else ( < term [MC] > )".
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
calculate |
< "if ([MCond]) |
||||
| then ([MC]) | |||||||
| else ([MC])" > | |||||||
|
|
|||||||
Beispiel:
e[1] = A; point; dragable; 1.0,3.0;
e[2] = B; point; dragable; 3.0,3.0;
e[3] = P; point; fixed; -3.0, 3.0;
e[4] = g; line; straightLine; B,A;
e[5] = m0; measure; calculate; "if (distance(P,g) < 0.05)
then (distance(A,B))
else (distance(A,P)+
distance(B,P))",
-5.0,10.0,"d(A,B) = ","";
2.4.4 Externe Funktionsbibliotheken / External function libraries
Externe Funktionsbibliotheken können durch die Unterklasse Function eingebunden werden. Die Funktionsbibliotheken müssen dabei als Java-Klassen vorliegen. Die Objektdaten bestehen dabei aus n Zeichenketten S1, ..., Sn mit 1 £ n £ 10. Vereinbarungsgemäß enthält S1 den Bezeichner der Klasse, die eingebunden werden soll. Die restlichen Zeichenketten können weitere Objektbezeichner oder numerische Werte enthalten, die als Parameter dienen.
External function libraries can be implemented using the subclass Function. The function libraries have to be in form of a Java-class. The object data is composed of n strings S1, ..., Sn where 1 £ n £ 10. Accordingly, S1 is given the object label of the class that is to be implemented. The remaining strings may include other object labels or numeric values, that can be used as parameters.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
function |
< S1 [s] > , |
||||
| < ... > , | |||||||
| < Sn [s] > | |||||||
|
|
|||||||
Beispiel:
e[1] = a; measure; controller; 5.0,5.0,1.0,3.0,"a = ","";
e[2] = b; measure; controller; 5.0,4.0,1.0,3.0,"b = ","";
e[3] = e; line; curve; "t","exp(calculate(a)*t+
calculate(b))", -8.0, 8.0, 50;
e[4] = x0; measure; calculate; "-100.0";
e[5] = x1; measure; calculate; "1.0";
e[6] = m0; measure; function; "Functional_Integral","e",
"x0","x1","50","simpson",4.0,3.0,
"Flächeninhalt = "," F.E.";
2.5 Interaktionselemente / Interaction Elements
2.5.1 Schieberegler / Slide controller
Schieberegler werden durch die Unterklasse Controller realisiert. Mit ihnen lassen sich numerische Werte aus einem vorgegebenen Intervall einstellen, die als Parameter für die Definition von geometrischen Objekten dienen können.Als Objektdaten sind anzugeben: ein Anfangswert a, die Schrittweite s, ein Intervall [x0, x1], die Breite b des Schiebereglers in Bildschirmpunkten sowie ein Präfix und Suffix zur Beschriftung.
Slide controllers are imlemented by the subclass Controller. They can be used to choose numeric values taken out of a given interval, which then can be used as parameters for the definition of geometric objects.
Objects data that have to be determined are: a starting value a, the increment s, an interval [x0, x1], horizontal size b of the slider in pixel and a prefix and suffix as a label.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
controller |
< Anfangswert a [d] > , |
||||
| < Schrittweite s [d] > , | |||||||
| < Intervallwert x0 [d] > , | |||||||
| < Intervallwert x1 [d] > , | |||||||
| < Breite b [i] > , | |||||||
| < Präfix [s] > , | |||||||
| < Suffix [s] > | |||||||
|
|
|||||||
Beispiel:
e[1] = a; measure; controller; 1.25,0.25,-1.0,5.0,50,"a = ","";
e[2] = b; measure; controller; 2.0,0.5,-1.0,5.0,50,"b = ","";
e[3] = e; line; curve; "t","exp(calculate(a)*t+
calculate(b))", -8.0, 8.0, 50;
2.5.2 Checkbox / Checkbox
Zweistufige Schaltelemente werden durch die Unterklasse Checkbox realisiert. Eine Checkbox kann lediglich die Werte 1 und 0 annehmen. Als Objektdaten ist ein Anfangswert und eine Beschriftung anzugeben.
Two-stage control elements are implemented by the subclass Checkbox. A checkbox can only assume the values 1 and 0. The object data that has to be provided are the beginning value and a label.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
checkbox |
< Beschriftung [s] > , |
||||
| < Anfangswert [i] > | |||||||
|
|
|||||||
Beispiel:
e[1]= cb1; measure; checkbox; "Hilfe zeigen",0; e[2]= cb2; measure; checkbox; "Lösung zeigen",0;
2.5.3 Schalter / Button
Ein Schalter kann durch die Unterklasse Button erzeugt werden. Durch das Anklicken eines Schalters mit der Computermaus wird ein Ereignis ausgelöst, das in den Objektdaten durch die Variable e bestimmt ist. Folgende Ereignisse sind möglich:- action: In Kombination mit dem move-Befehl (Seite
pageref) kann die Figur in einen
bestimmten Zustand versetzt werden.
- reset: Die Figur wird in den Anfangszustand zurückgesetzt.
- help: Ein Hilfetext wird angezeigt.
- evaluate: Die Antwortanalyse wird aufgerufen.
- clearTrace: Alle Ortsspuren werden gelöscht.
A switch can be created using the subclass Button. Clicking the switch with the computer mouse triggeres the event which has been predefined in the object data by the variable e. The following events are possible:
- action: In combination
with the move-command (page pageref) the figure can be set into a certain
state.
- reset: The figure is
reset to its beginning state.
- help: A help text will
be shown.
- evaluate: The analysis
of the answer is initiated.
- clearTrace: All traces are cleared.
|
|
|||||||
| Bezeichner |
Klasse |
Unterklasse |
Objektdaten |
||||
|
|
|||||||
|
< Name [s] > |
measure |
button |
< Beschriftung [s] > , |
||||
| < Ereignis e [s] > | |||||||
|
|
|||||||
Beispiel:
e[1] = b0; measure; button; "Hilfe","help"; e[2] = b1; measure; button; "Auswertung","evaluate"; e[3] = b2; measure; button; "Ortsspur löschen","clearTrace";
Chapter 3
Sonderfunktionen / Special Functions
3.1 Beschränken des Zustandsraums der Figur / Restricting the states of figures
Um den Zustandsraum einer Figur zu beschränken,
ist die Angabe einer Liste limit[1..n] erforderlich. Jeder Listeneintrag
definiert durch die Angabe einer Prüffunktion (Seite pageref)
einen Figurenzustand, den die Figur nicht einnehmen kann.
It is possible to limit the states a figure can assume. It can be
done by use of a list limit[1..n]. Each entry of the list
uses a function with boolean values (pageref) to define a state which the figure cannot
assume.
Beispiel / Example:
limit[1] = "distance(A,B) < 20" limit[2] = "isIncident(A,S)" limit[3] = "isIncident(B,S)"
3.2 Ein- und Ausblenden von Objekten
/
Showing and hiding objects
Mit Hilfe einer Liste hidden[1..n] können
Teile der Figur beim Eintreten bestimmter Figurenzustände ein- und ausgeblendet
werden. Jeder Listeneintrag besteht aus der Angabe einer Prüffunktion (Seite
pageref) und einer Anzahl von Objektbezeichnern.
Die angegebenen Objekte werden ausgeblendet, sobald die Prüffunktion den
Wert 1 annimmt.A list hidden[1..n]can be used to hide or show parts of a figure in specified constellations. Each entry in the list consists of a function with boolean values (pageref) and a number of object labels. The named objects will be hidden as soon as the function assumes a value of 1.
Beispiel / Example:
hidden[1] = "if (not(isIncident(A,B))) hide (k,Textbox_1)" hidden[2] = "if (calculate(f1) = 1) hide (A,B,C,D)"
3.3 Erzeugen von speziellen Figurenzuständen / Generating specific states of figures
Mit Hilfe einer Liste move[1..n] kann die Figur in einen bestimmten Zustand versetzt werden. Jeder Listeneintrag besteht aus der Angabe einer Prüffunktion (Seite pageref), eines Punktobjekts und Paares von Zielkoordinaten. Der spezielle Figurenzustand wird hergestellt, sobald die Prüffunktion den Wert 1 annimmt. Dann werden dem angegebenen Punktobjekt die definierten Zielkoordinaten zugewiesen.A list move[1..n]can be used to assign a specific state to a figure. Each entry of the list consists of a function with boolean values (pageref), a point object, and a pair of target coordinates. The specified state is assigned to the figure as soon as the function assumes the value 1. Then the the defined target coordinates are applied to the point object.
Beispiel / Example:
move[1] = "if (calculate(Button1)) move (A, -7.0, 0.0)" move[2] = "if (calculate(Button1)) move (B, 5.0, 0.0)" move[3] = "if (calculate(Button1)) move (S, 2.0, 0.0)"
3.4 Hilfen / Help
Abrufbare Hilfetexte werden in einem Skript in drei Schritten erzeugt:- Die Definition einer Hilfe beginnt mit dem Befehl <Help>.
- In den folgenden Zeilen können beliebig viele Hilfeinformationen stehen.
- Das Ende einer Hilfe wird mit </Help> festgelegt.
Helptexts are generated in a three step script:
- The definition starts with the command <Help>.
- The following lines may contain as much information as needed.
- The end of the helptext is marked with </Help>.
Beispiel / Example:
<Help> Der Schwerpunkt zweier Punktmassen teilt ihre Verbindungsstrecke im umgekehrten Teilverhältnis. </Help>
3.5 Textfenster / Textbox
Ein Textfenster auf der Zeichenfläche wird in vier Schritten erzeugt:- Die Definition eines Textfensters beginnt mit <TextBox> (früher: <ProblemText> oder <TextBoxBegin>).
- In der zweiten Zeile muß die Position auf der Zeichenfläche festgelegt werden. Dies geschieht durch Position = x; y; b; h; (früher: TextBox = x; y; b; h;). Dabei geben die Variablen x und y die Position der linken oberen Ecke in Fensterkoordinaten an. Die Variablen b und h legen die Breite und Höhe des Fensters in Bildschirmpunkten fest. Ist b = -1 und h = -1, so wird die Fenstergröße automatisch berechnet.
- Nach der Positionsangabe können optional Farbvariablen für die Beschriftungsfarbe, Rahmenfarbe und Füllfarbe angegeben werden. In den folgenden Zeilen stehen dann beliebig viele Textinformationen. Funktionale werden durch {<"Term" [MC]>} eingebunden.
- Das Ende eines Textfensters wird mit </TextBox> (früher: </Problem- Text> oder <TextBoxEnd>) angezeigt.
A textbox on the drawing area is generated in four steps:
- The definition of the textbox starts with <TextBox> (previously: <ProblemText> or <TextBoxBegin>).
- The second line designates the box's position in the drawing area. This is done by the use of Position = x; y; b; h; (previously: TextBox = x; y; b; h;). The variables x and y are for the position of the upper left corner of the box using coordinates of the window. The variables b and h designate the horizontal and vertical dimensions of the window in pixels. The dimensions of the textbox are calculated automatically if b = -1 and h = -1.
- After setting the postition, optionally variables can be set to specify font color, border color, and background color. In the following lines any number of text infomation can be given. Functions can be included using {<"Term" [MC]>}.
- The end of a textbox is marked by </TextBox> (previously: </ProblemText> or <TextBoxEnd>).
Beispiel / Example:
<TextBox>
Position = 20;20;200;100
{nameColor = black}
{edgeColor = 255,225,255}
{faceColor = white}
Dieses Textfenster wird auf
der Zeichenfläche angezeigt.
A = ({"coordinateX(A)"}, {"coordinateY(A)"})
</TextBox>
3.6 Bilder / Pictures
Mit Hilfe des image-Befehls können Bilddateien eingebunden und auf der Zeichenfläche angezeigt werden. Neben dem Dateinamen ist dazu eine Koordinatenposition anzugeben. Diese kann absolut durch die Angabe von x- und y-Koordinaten definiert sein oder es wird ein Punkt angegeben, an dessen Position die Bilddatei dargestellt wird. Wird der Punkt bewegt, so verschiebt sich auch die Grafik.It is possible to implement pictures into the drawing area using the command image. The name of the picture-file has to be given and in addition coordinates have to be assigned for the picture to be shown. These coordinates can be provided giving x- and y-coordinates or a point can be named. In the latter case, the picture will be displayed at the points position. If the point is then moved, the picture will move as well.
Beispiel / Example:
image[1] = "Formel01.gif", 20, 100 image[2] = "Formel02.gif", 70, 120
3.7 Antwortanalyse / Response Analysis
Die Definition einer Antwortanalyse in einem Skript ist unterteilt in einen Hauptabschnitt und mehrere Unterabschnitte.In dem Hauptabschnitt wird die Gesamthöchstzahl MAX_ANSWER von
möglichen Antwortversuchen festgelegt. Wird der Wert auf 0 gesetzt, so
hat der Schüler unbegrenzt viele Antwortversuche. Ferner ist im Hauptabschnitt
eine Liste condition[1..n] von Prüffunktionen (Seite pageref) anzugeben. Der Hauptabschnitt
wird durch die beiden Befehle <Problem> und </Problem>
umschlossen.
The definition of an answer analysis in a script is subdivided into a
main section and several subsections.
In the main section the maximum number of attempts to answer MAX_ANSWER
can be set. If the value is set to 0 then the student can try to
answer as often as he likes. In addition, a list condition[1..n]
with functions with boolean values (pageref) has to be included. The main section is
enclosed by the two commands <Problem> and </Problem>.
Beispiel / Example:
<Problem>
MAX_ANSWER = 3
condition[1] = "calculate(r) < 0.26"
condition[2] = "calculate(r) > 0.24"
condition[3] = "calculate(r) < 0.51"
condition[4] = "calculate(r) > 0.49"
</Problem>
In jedem Unterabschnitt wird jeweils ein Antwortwert und eine zugehörige
Liste von Antwortkommentaren definiert. Zur Beschreibung eines Antwortwerts
gehört die Angabe eines Prüfschlüssels key, der durch eine boolesche
Verknüpfung der im Hauptabschnitt definierten Prüffunktionen festgelegt
wird. Die Antwortkommentare werden in einer Liste commment[1..h]
beschrieben. In einem Skript steht pro Kommentar nur eine Zeile zur Verfügung.1 Bei der Ausgabe eines Kommentars wird ein
Zeilenumbruch durch den Befehl /n bewirkt. Jeder Unterabschnitt
zur Definition eines Antwortwerts wird durch die beiden Befehle <Answer
i> und </Answer i> umschlossen.In every subsection there is the definition of a value of an answer and an accompanying list of comments to the answers. The description of an answer value has to include an answering key key which is defined by a boolean link. This boolean link is determined by the boolean function of the main section. The comments to the answers are described in the list commment[1..h]. In a script only one line may be used per comment.1 If a line break is to be used when displaying the comment, it can be inserted using the command /n. Each subsection of the definitions of an answer value is enclosed by the commands <Answer i> and </Answer i>.
Beispiel / Example:
<Answer 1>
key = "condition[1] AND condition[2]"
comment[1] = "Richtig. Der Eckenschwerpunkt teilt die
Verbindungsstrecke zweier Punktmassen im
umgekehrten Verhältnis der anliegenden Massen."
</Answer 1>
<Answer 2>
key = "condition[3] AND condition[4]"
comment[1] = "Ihre Antwort ist nicht richtig. Der Eckenschwer-
punkt würde nur dann genau in der Mitte zwischen
zwei Punktmassen liegen, wenn diese gleich groß
wären. Versuchen Sie es noch einmal."
comment[2] = "Ihre Antwort ist immer noch nicht richtig.
Lösung: Der Eckenschwerpunkt teilt die Verbin-
dungsstrecke zweier Punktmassen im umgekehrten
Verhältnis der anliegenden Massen."
</Answer 2>
<Answer 3>
key = "1"
comment[1] = "Ihre Antwort ist nicht richtig. Versuchen Sie es
noch einmal."
comment[2] = "Ihre Antwort ist immer noch nicht richtig.
Lösung: Der Eckenschwerpunkt teilt die Verbin-
dungsstrecke zweier Punktmassen im umgekehrten
Verhältnis der anliegenden Massen."
</Answer 3>
3.8 Animationen / Animations
Durch den animation-Befehl kann eine Figur automatisch bewegt werden. Dazu ist ein Punkt <PointObject> der Klasse Dragable anzugeben. Das Bezugsobjekt von diesem Punkt muß dabei entweder eine Strecke, eine Gerade, ein Kreis, ein Polygon oder eine Kurve sein und dient als Führungslinie. Ferner ist die Angabe einer Bewegungsrichtung (1 oder 0), einer Geschwindigkeitsverzögerung (in msec) und einer Anzahl von Animationsschritten erforderlich. Jede Animation wird durch einen (automatisch erzeugten) Schalter ein- und ausgeschaltet. Soll die Animation gleich beim Aufrufen der Figur gestartet werden, so ist als letzter Parameter der Wert 1 anzugeben, falls nicht, der Wert 0.The command animation makes it possible to move a figure automatically. A point <PointObject> of the class Dragable has to be determined in order to do that. The corresponding object to the point has to be a line segment, a straight line, a circle, a polygon, or a curve. It serves as a guiding line. In additon, the direction of the movement (1 or 0), the ratio of the change of velocity (in msec), and the number of steps for the animation has to be set as well. Every animation can be toggled by a switch (which is generated automatically). If the last parameteris set to 1 then the animation is started as soon as the figure is called for, if it is set to 0 it will not start right away.
Beispiel / Example:
animation = "A,0,10,200,0"
Chapter 4
Systemeinstellungen / Systemproperties
4.1 Variablen / Variables
Mit Hilfe der Systemvariablen können die globalen Einstellungen von Geometria festgelegt werden. In der Regel sind diese Variablen in der Layout-Vorlage definiert. Um Ausnahmen in einzelnen Skripten zu realisieren, können die Systemvariablen aber auch in jedem Skript überschrieben werden.The global properties of Geometria can be set using system variables. As a rule these varables are defined in the layout-preset. To implement exceptions these system varables can be overwritten in any skript.
|
|
|||||
| Systemvariable / System Variable |
Default-Wert / |
Beschreibung / |
|||
|
|
|||||
|
APPLET_WIDTH = < [i] > |
640 |
Breite der Zeichenfläche in Bildschirmpunkten / Width of the drawing plane in pixels |
|||
|
|
|||||
|
APPLET_HEIGHT = < [i] > |
480 |
Höhe der Zeichenfläche in Bildschirmpunkten / Height of the drawing plane in pixels |
|||
|
|
|||||
|
WORLD_X_MAX = < [d] > |
+16.0 |
Größter x-Wert im Weltkoordinatensystem |
|||
|
|
|||||
|
WORLD_X_MIN = < [d] > |
-16.0 |
Kleinster x-Wert im Weltkoordinatensystem |
|||
|
|
|||||
|
WORLD_Y_MAX = < [d] > |
+12.0 |
Größter y-Wert im Weltkoordinatensystem |
|||
|
|
|||||
|
WORLD_Y_MIN = < [d] > |
-12.0 |
Kleinster y-Wert im Weltkoordinatensystem |
|||
|
|
|||||
|
FONT = < [s] > |
Serif |
Schriftart |
|||
|
|
|||||
|
FONTSIZE = < [i] > |
10 |
Schriftgröße |
|||
|
|
|||||
|
|
|||||
| Systemvariable |
Default-Wert |
Beschreibung |
|||
|
|
|||||
|
GRIDSIZE = < [i] > |
10 |
Rasterabstand in Bildschirmpunkten |
|||
|
|
|||||
|
GRIDCOLOR = < [c] > |
235,205,180 |
Farbe des Hintergrundrasters |
|||
|
|
|||||
|
BACKGROUNDCOLOR = < [c] > |
235,225,200 |
Farbe der Zeichenfläche |
|||
|
|
|||||
|
APPLETBGCOLOR = < [c] > |
black |
Farbe des Applethintergrunds |
|||
|
|
|||||
|
CONTROLPANELCOLOR = < [c] > |
black |
Farbe des Hintergrunds der Interaktionselemente |
|||
|
|
|||||
|
TITLE = < [i] > |
Name der Skriptdatei |
Titel des Betrachterfensters |
|||
|
|
|||||
|
SHOWLABEL = < [b] > |
false |
Beschriftungen anzeigen |
|||
|
|
|||||
|
SHOWGRID = < [b] > |
false |
Hintergundraster anzeigen |
|||
|
|
|||||
|
SHOWAXIS = < [b] > |
false |
Koordinatenachsen anzeigen |
|||
|
|
|||||
|
SNAPTOGRID = < [b] > |
false |
Rasterfangmodus einschalten |
|||
|
|
|||||
|
ALLPOINTSDRAGABLE = < [b] > |
false |
Verschieben nicht-ziehbarer Punkte |
|||
|
|
|||||
|
LANGUAGE = < [s] > |
GERMAN |
Beschriftungssprache (GERMAN oder ENGLISH) |
|||
|
|
|||||
|
USESEPARATEWINDOW = < [b] > |
true |
Zeichenfläche in separatem Fenster darstellen |
|||
|
|
|||||
|
|
|||||
| Systemvariable |
Default-Wert |
Beschreibung |
|||
|
|
|||||
|
HIDEMENU( < [s] > ) |
|
Ausblenden eines Menüs (Menübezeichner angeben) | |||
|
|
|||||
|
HIDEMENUITEM( < [s] > ) |
|
Ausblenden eines Menüpunkts (Menüpunktbezeichner angeben) | |||
|
|
|||||
|
MEASURE_EXACTNESS = < [i] > |
3 |
Nachkommastellen bei Funktionalen |
|||
|
|
|||||
|
CHECKSYMBOLS = < [b] > |
false |
Griechische Buchstaben darstellen |
|||
|
|
|||||
|
DRAGMEASURE = < [b] > |
false |
Funktionale auf der Zeichenfläche ziehbar |
|||
|
|
|||||
|
INERTUPDATEMODE = < [b] > |
true |
Trägheitsmodus in der update-Methode einschalten |
|||
|
|
|||||
4.2 Farbdefinitionen
Um Farben zu definieren, sind zwei alternative Wege vorgesehen. Als erstes kann eine Farbe durch die Angabe eines Zahlentripels r, g, b definiert werden, mit 0 £ r, g, b £ 255. Dabei bestimmt r den Rotanteil, g den Grünanteil und b den Blauanteil einer Farbe.Die zweite Möglichkeit besteht darin, einen der vordefinierten Farbbezeichner zu verwenden: black (schwarz), blue (blau), cyan (türkisblau), darkGray (dunkelgrau), gray (grau), green (grün), lightGray (hellgrau), magenta (violett), orange (orange), pink (rosa), red (rot), white (weiß), yellow (gelb), random (Zufallsfarbe), brighter (heller als der Hintergrund) und darker (dunkler als der Hintergrund).
Soll eine Farbe nicht definiert werden, so ist der Wert 0 anzugeben.
There are two alternative ways to define a color value. The first possibility is to use the rgb-scheme by a triple of numbers r, g, b separated by commata, where 0 £ r, g, b £ 255.
The second way is to use a predefined color value, like: black , blue, cyan, darkGray, gray, green, lightGray, magenta, orange, pink, red, white, yellow, random (a randomly chosen color), brighter (as the background) and darker (as the background).
If no special color should be defined, use the value 0.
4.3 Punktformen / Point Shapes
Um Punkte auf der Zeichenfläche darzustellen, kann zwischen sechs vordefinierten Formen gewählt werden: smallsquare (kleines Quadrat), square (mittleres Quadrat), bigsquare (großes Quadrat), smallcircle (kleiner Kreis), circle (mittlerer Kreis) und bigcircle (großer Kreis). Die Angabe von default bewirkt, daß die in der aktuellen Layout-Vorlage festgelegte Punktform verwendet wird.It is possible to choose from six different shapes when displaying points in the drawing area: smallsquare, square (medium-sized), bigsquare, smallcircle, circle (medium-sized), and bigcircle.
4.4 Sonderzeichen / Special Characters
Alle Beschriftungen oder Objektbezeichner können Buchstaben des griechischen Alphabets enthalten. Um den Parser zu veranlassen, gezielt nach Sonderzeichen zu suchen, ist es erforderlich, daß die Systemvariable CHECKSYMBOLS in dem betreffenden Skript auf true gesetzt wird.Characters of the Greek alphabet can be used as labels. To have the parser search for the special characters it is necessary to set the system variable CHECKSYMBOLS of the appropriate script to true.
Es können folgenden Zeichen erzeugt werden / The following chars can
be generated:
\alpha (a), \beta (b),
\gamma (g), \delta (d), \epsilon
(e), \zeta (z), \eta (h), \theta
(q), \jota (i), \kappa (k), \lambda
(l), \my (m), \ny (n), \xi
(x), \omikron (o), \pi (p),
\rho (r), \sigma (s), \tau
(t), \ypsilon (u), \phi (f), \chi
(c), \psi (y), \omega (w), \ALPHA
(A), \BETA (B), \GAMMA (G), \DELTA (D), \EPSILON
(E), \ZETA (Z), \ETA (H), \THETA (Q),
\JOTA (I), \KAPPA (K), \LAMBDA (L),
\MY (M), \NY (N), \XI (X), \OMIKRON (O), \PI (P), \RHO (P), \SIGMA (S), \TAU (T), \YPSILON (U), \PHI (F), \CHI
(X), \PSI (Y) und \OMEGA (W).
4.5 Applet-Parameter
Beim Einbinden des Applets Geometria in ein HTML-Dokument können folgende Parameter übergeben werden.- script: Bezeichnet den Dateinamen des Skripts, das eingelesen werden soll.
- style: Bezeichnet den Dateinamen der Layout-Vorlage, die eingelesen werden soll.
- backgroundColor: Legt die Farbe des Applet-Hintergrunds fest.
- startButton: Legt fest, ob ein Button erzeugt werden soll, durch den man Geometria startet, oder ob das Applet direkt ausgeführt werden soll.
- scriptPath: Legt das Verzeichnis fest, in dem die Skriptdatei gespeichert ist.
- stylePath: Bestimmt das Verzeichnis, in dem die Layout-Vorlage abgelegt ist.
- imagePath: Gibt das Verzeichnis an, in dem alle Bilddateien
(s. Seite pageref) gespeichert
sind.
When Geometria is inplemented as an applet in an HTML-documentkument, the following parameters can be passed on:
- script: names the file of the script which is to be read
- style: names the file of the layout-preset which is to be read
- backgroundColor: designates applet's background color
- startButton: decides whether a button is created that can be used to start Geometria, or whether the applet starts directly
- scriptPath: designates the folder in which the script file is saved
- stylePath: designates the folder in which the layout-preset is stored
- imagePath: designates the folder in which the pictures (see page pageref) are stored
Beispiel / Example:
<applet code="Geometria" codebase="" archive="Geometria.jar"
height="395" width="480">
<param name="script" value="demo.script">
<param name="style" value="default.style">
<param name="startButton" value="0">
<param name="backgroundColor" value="100,23,00">
<param name="scriptPath" value="./script/">
<param name="stylePath" value="./style/">
<param name="imagePath" value="./image/">
</applet>
Abkürzungsverzeichnis / Glossary of Abbreviations
[b] boolescher Wert / boolean value (true, false)
[c] Farbdefinition / Color definition (Seite / page pageref)
[d] reelle Zahl / real number (z. B. / e.g. -1.2)
[i] ganze Zahl / integer (z. B. / e.g. 1, -2)
[s] Zeichenkette / String (''Text'')
[C] Kreisobjekt / Circle (Seite / page pageref)
[SE] Kreisbogenobjekt / Arc of a Circle (Seite/ page pageref)
[CO] Koordinatensystem / Coordinate System (Seite / page pageref)
[CU] Kurvenobjekt / Curve (Seite / page pageref)
[M] Funktional / Function (Seite / page pageref)
[MC] Term (Seite / page pageref)
[MCond] Prüffunktion / Function with Boolean Values (Seite
/ page pageref)
[L] Strecken-, Strahlen- oder Geradenobjekt / Line Segment,
Ray, Line (Seite / page pageref)
[LO] Ortslinienobjekt / Locus (Seite / page pageref)
[P] Punktobjekt / Point (Seite / page pageref)
[PG] Polygonobjekt / Polygon (Seite / page pageref)
[PS] Punktmengenobjekt / Point Set (Seite / page pageref)
[R] Strahlenobjekt / Ray (Seite / page pageref)
[ST] Geradenobjekt / Straight Line (Seite / page pageref)
Footnotes:
1In
dem unten aufgeführten Beispiel sind aus Platzgründen Zeilenumbrüche eingefügt.